ملخص الدرس / الرابعة متوسط/رياضيات/الأنشطة الهندسية/نظرية طالس
الملخص
من الأستاذ(ة) ELBEY Mouloudنظرية طالس
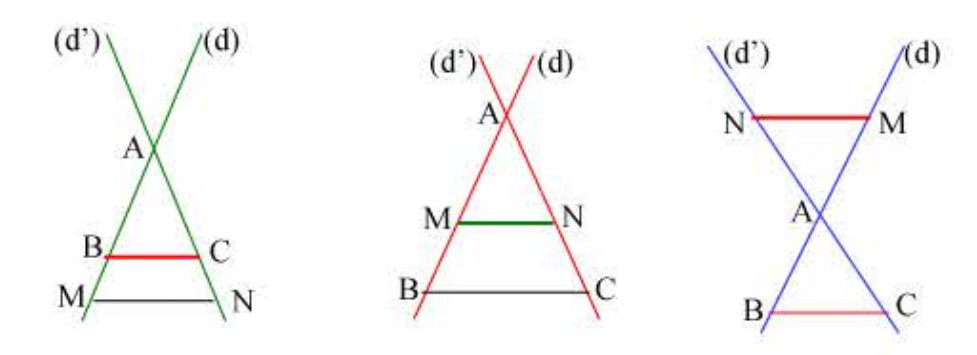
1) نظرية طالس:
و
مستقيمان في
.
و
نقطتان من
تختلفان عن
.
و
نقطتان من
تختلفان عن
.
إذا كان المستقيمان و
متوازيان فإن:
أطوال المثلث
و أطوال المثلث
.
ملاحظة:
نظرية طالس هي وسيلة لحساب الأطوال.
تذكير:
لتطبيق نظرية طالس يجب:
1) التأكد من استقامية النقط و النقاط
.
2) والتأكد من التوازي بين مستقيمين، مثلاً: و
.
وفيمايلي فيديوا تعليمي حول الدرس:
وفيمايلي فيديوا تعليمي لتمرين تطبيقي حول الدرس:
النظرية العكسية لنظرية طالس
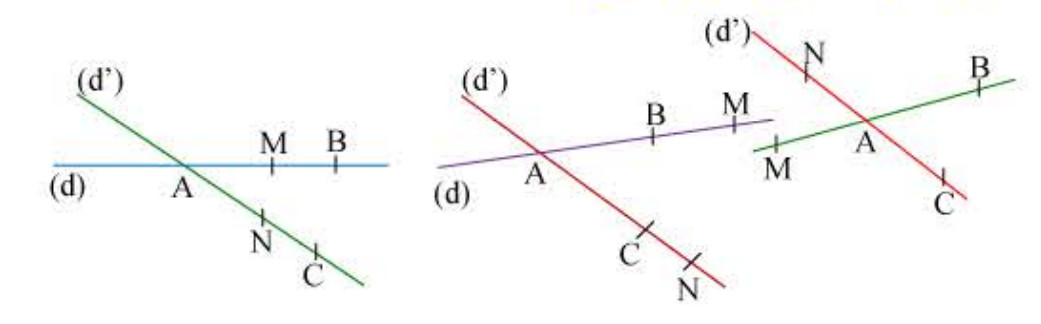
2) النظرية العكسية:
و
مستقيمان متقاطعان في
.
و
نقطتان من
تختلفان عن
.
و
نقطتان من
تختلفان عن
.
إذا كان والنقاط
والنقاط
إستقامية وبنفس الترتيب فإن
و
متوازيان.
ملاحظات:
- نظرية طالس العكسية هي وسيلة لكي نبين أن مستقيمين متوازيان.
- مهم جدا التأكد من استقامية النقط وبنفس الترتيب عند تطبيق النظرية العكسية نظرية طالس.
تقسيم قطعة مستقيم هندسيا
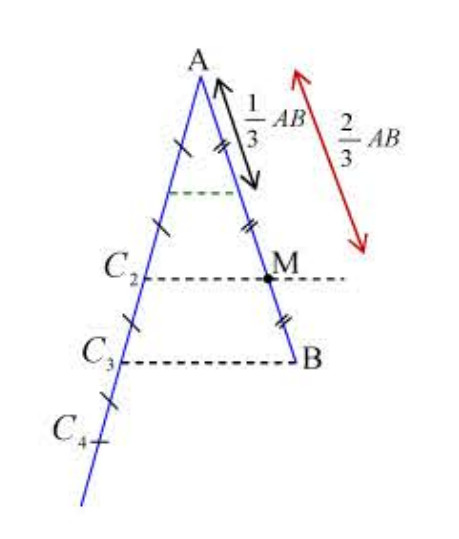
3) تقسيم قطعة مستقيم هندسيا:
مثال:
عين النقطة من
بحيث
.
لتعيين النقطة من
تتبع المراحل الآتية:
- نرسم نصف مستقيم مدرج تدريجيا منتظما بالمدور.
- نصل بين النقطتين و
.
المستقيم يقطع
في النقطة
بحيث:
.