ملخص الدرس / الرابعة متوسط/رياضيات/الأنشطة العددية/المعادلات و المتراجحات من الدرجة الاولى بمجهول واحد

1) حل معادلة من الدرجة الأولى ذات مجهول واحد:

خاصية:

حل معادلة من الدرجة الأولى بمجهول واحد ن تؤول إلى حل معادلة من الشكل .

- إذا كان  فإن المعادلة تقبل حلا واحدا: 

مثال:

حل المعادلة 

نحول الأعداد المجهولة إلى الطرف الأول ونحول الأعداد المعلومة إلى الطرف الثاني.

فيكون لدينا  أي  إذن 

فيديو تعليمي لتمرين تطبيقي حول الدرس:

فيديوا تعليمي حول الدرس:

2) حل معادلة من الشكل : (ax+b)(x+d)

خاصية (01):

جداء عاملين معدوم يعني أن أحد هاذين العاملين على الأقل معدوم.

خاصية (02):

 أعداد حقيقية بحيث :  و  حل المعادلة.

 معناه حل المعادلتين

 و 

مثال:

حل المعادلة: 

 معناه:

إما :  أي  ومنه 

أو :  أي  ومنه 

3) حل معادلة يؤول حلها إلى حل معادلة جداء معدوم:

مثال:

حل المعادلة: 

لحل هذه المعادلة أول مرحلة هي : تحليل المجموع الجبري على شكل جداء عاملين.

 عامل مشترك 

تبسيط الجداء:

حل المعادلتين:

معناه:

إما :  أي 

أو :  أي 

إذن المعادلة تقبل حلين وهما :  و .

4) مفهوم المتراجحة:

كل علاقة من الشكل:

، 

 ، 

بحيث:  هو العدد المجهول و ،  عددان حقيقيان بحيث .

تسمى متراجحة من الدرجة الأولى بمجهول واحد.

5) حل متراجحة:

تعريف:

حل متراجحة هو إيجاد كل قيم العدد المجهول التي من أجلها تكون المتباينة صحيحة، هذه القيم تسمى حلول هذه المتراجحة.

مثال:

حل المتراجحة الآتية: 

ومنه:  (نجمع المجاهيل في الطرف الأول والأعداد المعلومة في الطرف الثاني للمتراجحة).

ومنه: 

حذار: بما أن  فإن  ومنه .

إذن كل قيم  الأكبر من 2 هي حلول للمتراجحة.

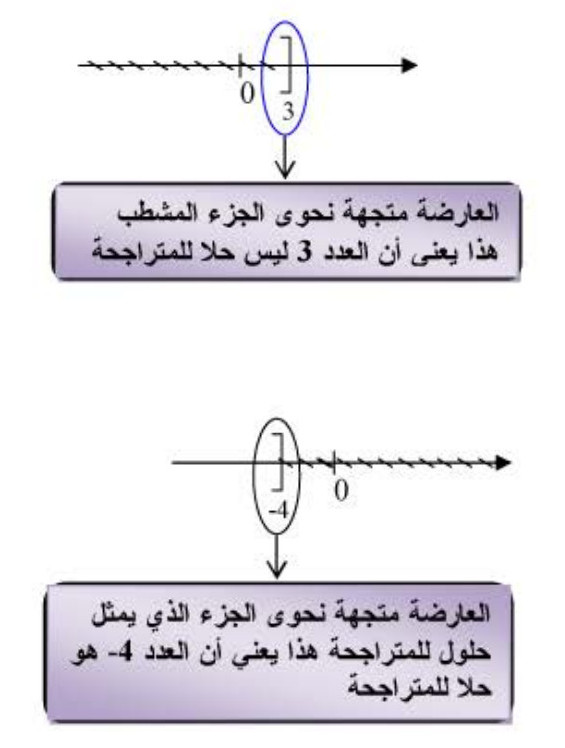
3) تمثيل حلول متراجحة:

- تمثل مجموعة حلول المتراجحة بيانيا بمستقيم عددي.

- معظم المتراجحة تقبل عددا غير منته من الحلول.

حذار: 

- المتراجحة  تقبل كل الأعداد حلولاً لها لأنه مهما تكون قيمة  فإن المتراجحة صحيحة.

- المتراجحة  لا تقبل حلولاً لأنه لا توجد قيم لـ :  بحيث يكون .

مثال (01) (لاحظ الشكل 01):

التمثيل البياني لحلول المتراجحة .

- أعداد تمثل حلولاً للمتراجحة.

- أعداد ليست حلولاً للمتراجحة.

مثال (02) (لاحظ الشكل 02):

التمثيل البياني لحلول المتراجحة