ملخص الدرس / الرابعة متوسط/رياضيات/الدوال و تنظيم المعطيات/التناسبية – الدالة الخطية و الدالة التألفية
الملخص
من الأستاذ(ة) ELBEY Mouloudالدالة الخطية
1) الدالة الخطية:
تعريف:
عندما نرفق كل عدد بالجداء حيث
عدد طبيعي معلوم، نقول أننا عرفنا دالة خطية.
نرمز لها بـ:
هي صورة
بالدالة
ونكتب :
.
مثال (01):
دالة خطية معاملها
، أوجد العدد
إذا علمت أن :
الحل :
لدينا: دالة خطية معاملها
معناه:
.
لدينا: معناه
أي
إذن:
.
مثال (02):
دالة خطية معاملها
.
1- أوجد صورة العدد بالدالة
.
2- ما هو العدد الذي صورته بواسطة الدالة
.
الحال:
1- دالة خطية معاملها
معناه
.
ومنه أي
.
إذن العدد هو صورة العدد
بالدالة
.
2- لدينا: ولدينا
.
إذن أي
ومنه
.
إذن العدد صورته هي العدد
بالدالة
.
فيديوا تعليمي حول الدرس :
فيديوا تعليمي حول الدرس:
التمثيل البياني لدالة خطية
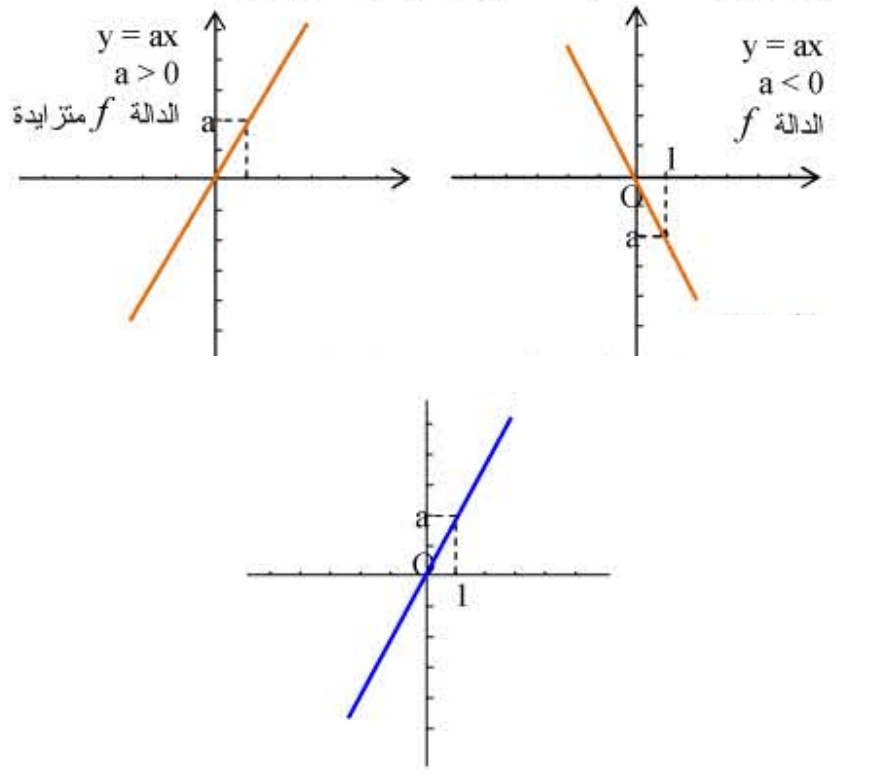
2) التمثيل البياني لدالة خطية:
التمثيل البياني لدالة خطية معاملها هي مجموعة النقط التي إحداثياها
أي
.
خاصية:
في معلم التمثيل البياني لدالة خطية معاملها
هو المستقيم الذي يشمل نقطة المبدأ والنقطة
التي إحداثياها
تعريف:
نقول : هي معادلة مستقيم بيان الدالة الخطية التي معاملها
.
العدد يسمى معامل التوجيه للمستقيم.
مثال (01) : لاحظ الشكل (01)
التمثيل البياني لدالة خطية معاملها أي
مثال (02): لاحظ الشكل (02)
تعين معامل الدالة الخطية إنطلاقا من تمثيلها البياني:
لدينا : أي
.
لإيجاد العدد يكفي أن نبحث عن صورة العدد 1 بالدالة
.
من خلال التمثيل لدينا:
صورة العدد 1 هي العدد 2.
إذن : أي
ومنه
.
التناسبية والدالة الخطية

3) التناسبية والدالة الخطية:
إليك جدول تناسبية (لاحظ الشكل)
معامل المتناسبية هو معامل الدالة الخطية
.
أي أو
فيمايلي فيديوا تعليمي حول الدرس:
الدالة التآلفية:
4) الدالة التآلفية:
تعريف:
،
عددان معلومان.
عندما نرفق كل عدد بالجداء
، حيث
عدد معطى، ثم نضيف إلى ذلك الجداء عددا معلوما
نقول أننا عرفنا دالة تآلفية.
ونكتب : نسمي
صورة
بالدالة
ونكتب:
.
مثال:
هي الدالة التآلفية التي ترفق بكل عدد
العدد:
.
معناه: .
صورة هي
أي
إذن :
.
ملاحظة:
الدالة الخطية هي حالة خاصة للدالة التآلفية.
- لتكن دالة تآلفية بحيث :
فإن تغيرات
متناسبة مع تغيرات
ومعامل التناسبية هو المعامل
بحيث:
مع
.
مثال:
عين الدالة التآلفية علما أن :
و
.
الحل:
نعين الدالة التآلفية معناه إيجاد العددين
و
لدينا:
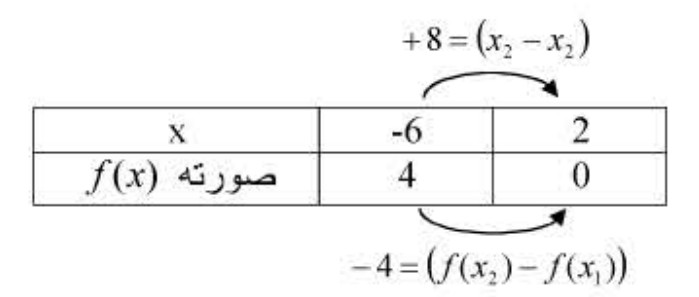
(لاحظ الشكل).
حساب معامل الدالة التآلفية
:
إذن
ومنه:
حساب العدد :
لدينا: معناه
أي
.
ومنه: إذن
.
ملاحظة:
يمكن إيجاد العددين و
وهذا بحل جملة معادلتين.
التمثيل البياني لدالة تآلفية
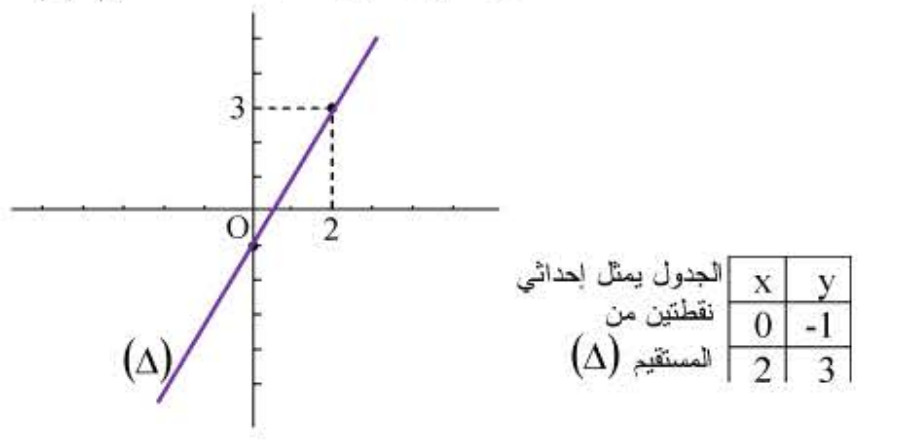
5) التمثيل البياني لدالة تآلفية:
تعريف:
التمثيل البياني لدالة تآلفية حيث: هو مجموعة النقاط التي إحداثياها
بحيث :
وهي معادلة مستقيم بيان الدالة التآلفية
.
- العدد يسمى معامل التوجيه للمستقيم.
- العدد يسمى الترتيب إلى المبدأ.
مثال:
مثل بيانيا الدالة التآلفية بحيث:
.
لتمثيل بيانيا الدالة يكفي تعيين نقطتين منه.
لدينا: معناه
وهي معادلة المستقيم
بيانيا الدالة
.
لدينا : .
إذا كان : فإن
.
إذا كان: فإن
* لاحظ الشكل.
فيديوا تعليمي لوضعية إدماجية: