ملخص الدرس / الثآنية ثانوي/رياضيات/الهندسة/المرجح

الدرس

مرجح نقطتين

تعريف مرجح نقطتين :

تعريف :

لتكن $A$ و $B$ نقطتين متمايزتين و ليكن $\alpha$ و $\beta$ عددين حقيقيين حيث $\alpha +\beta \neq 0$ .

نسمي مرجح النقطتين $A$ و $B$ المرفقتين بالمعاملين $\alpha$ و $\beta$ على الترتيب النقطة $G$ حيث : $\alpha \overrightarrow{GA}+\beta \overrightarrow{GB}= \vec{0}$ .

ملاحظة :

إذا كان $\alpha = \beta$ نحصل $\overrightarrow{GA}= -\overrightarrow{GB}$ و النقطة $G$ منتصف القطعة $\left [ AB \right ]$ تسمى عندئذ $G$ مركز المسافتين المتساويتين للنقطتين $A$ و $B$ و في هذه الحالة نأخذ $\alpha = \beta=1$ .

مبرهنة $1$ :

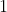إذا كانت النقطة $G$ مرجح النقطتين $A$ و $B$ و المرفقتين بالمعاملين $\alpha$ و $\beta$ على الترتيب فإن النقطة $G$ وحيدة .

خواص :

$.1$ إذا كانت النقطة $G$ مرجح الجملة المثقلة $\left \{ \left ( A,\alpha \right );\left ( B,\beta \right ) \right \}$ . فإن $G$ مرجح الجملة المثقلة $\left \{ \left ( A,k\alpha \right );\left ( B,k\beta \right ) \right \}$ . حيث $k$ عدد حقيقي غير معدوم .

$.2$ إذا كانت النقطة $G$ مرجح الجملة المثقلة $\left \{ \left ( A,\alpha \right );\left ( B,\beta \right ) \right \}$ . فإن النقط $A$ ، $B$ و $G$ على استقامة واحدة .

مبرهنة 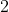$2$ :

إذا كانت النقطة $G$ مرجح النقطتين $A$ و $B$ و المرفقتين بالمعاملين $\alpha$ و $\beta$ على الترتيب فإن من أجل كل نقطة $M$ $\alpha \overrightarrow{MA}+\beta \overrightarrow{MB}=\left ( \alpha +\beta \right ) \overrightarrow{MG}$

ملاحظة :

إذا كان المرجح $G$ منتصف القطعة $\left [ AB \right ]$ فإن من أجل كل نقطة $M$ : $\overrightarrow{MA}+\overrightarrow{MB}=2 \overrightarrow{MG}$ .

مرجح ثلاث نقط

تعريف مرجح ثلاث نقط :

تعريف :

لتكن $A$ ، $B$ و $C$ ثلاث نقط و ليكن $\alpha$ ، $\beta$ و $\gamma$ أعداد حقيقية حيث $\alpha +\beta+\gamma \neq 0$ .

نسمي مرجح النقط $A$ ، $B$ و $C$ المرفقة بالمعاملات $\alpha$ ، $\beta$ و $\gamma$ على الترتيب النقطة $G$ حيث : $\alpha \overrightarrow{GA}+\beta \overrightarrow{GB}+\gamma \overrightarrow{GC}= \vec{0}$ .

مبرهنة $1$ :

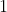إذا كانت النقطة $G$ مرجح للنقط $A$ ، $B$ و $C$ المرفقة بالمعاملات $\alpha$ ، $\beta$ و $\gamma$ على الترتيب النقطة $G$ وحيدة .

خاصية :

إذا كانت النقطة $G$ مرجح الجملة المثقلة $\left \{ \left ( A,\alpha \right );\left ( B,\beta \right );\left ( C,\gamma \right ) \right \}$ . فإن $G$ مرجح الجملة المثقلة $\left \{ \left ( A,k\alpha \right );\left ( B,k\beta \right );\left ( C,k\gamma \right ) \right \}$ .

حيث $k$ عدد حقيقي غير معدوم .

مبرهنة 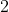$2$ :

إذا كانت النقطة $G$ مرجح النقط $A$ ، $B$ و $C$ المرفقة بالمعاملات $\alpha$ ، $\beta$ و $\gamma$ على الترتيب فإن من أجل كل نقطة $M$ ،

$\alpha \overrightarrow{MA}+\beta \overrightarrow{MB}+\gamma \overrightarrow{MC} =\left ( \alpha +\beta+\gamma \right ) \overrightarrow{MG}$ .

خاصية التجميع :

مبرهنة :

$G$ مرجح للنقط $A$ ، $B$ و $C$ المرفقة بالمعاملات $\alpha$ ، $\beta$ و $\gamma$ على الترتيب .

إذا كان $\alpha +\beta \neq 0$ و كانت $D$ مرجح النقطتين $A$ و $B$ المرفقتين بالمعاملين $\alpha$ و $\beta$ على الترتيب .

فإن $G$ مرجح النقطتين $D$ و $C$ المرفقتين بالمعاملين $\alpha+\beta$ و $\gamma$ على الترتيب .

إحداثيات مرجح ثلاث نقط

مبرهنة :

المستوي منسوب إلى معلم $\left ( O,\vec{i},\vec{j} \right )$ . لتكن النقطة $G$ مرجح للنقط $A$ ، $B$ و $C$ المرفقة بالمعاملات $\alpha$ ، $\beta$ و $\gamma$ على الترتيب .

نضع $A\left ( x_{A};y_{A} \right )$ ، $B\left ( x_{B};y_{B} \right )$ و $C\left ( x_{C};y_{C} \right )$ إحداثيا النقطة $G$ هي $\left ( x_{G},y_{G} \right )$ حيث :

$x_{G}=\frac{\alpha x_{A}+\beta x_{B}+\gamma x_{C}}{\alpha +\beta +\gamma }$ و $y_{G}=\frac{\alpha y_{A}+\beta y_{B}+\gamma y_{C}}{\alpha +\beta +\gamma }$

ملاحظة :

إذا كانت النقطة $G$ مرجح النقطتين $A$ و $B$ و المرفقتين بالمعاملين $\alpha$ و $\beta$ على الترتيب . و كان :

$A\left ( x_{A};y_{A} \right )$ ، $B\left ( x_{B};y_{B} \right )$ و $G\left ( x_{G};y_{G} \right )$ فإن :

$x_{G}=\frac{\alpha x_{A}+\beta x_{B}}{\alpha +\beta }$ و $y_{G}=\frac{\alpha y_{A}+\beta y_{B}}{\alpha +\beta }$

حالات خاصة :

$(1$ إذا كانت النقطة $G$ منتصف القطعة $\left [ AB \right ]$ .

$x_{G}=\frac{ x_{A}+ x_{B}}{2}$ و $y_{G}=\frac{ y_{A}+ y_{B}}{2 }$

$(2$ إذا كانت النقطة $G$ مركز ثقل المثلث $ABC$ .

$x_{G}=\frac{ x_{A}+ x_{B}+x_{C}}{3}$ و $y_{G}=\frac{ y_{A}+ y_{B}+y_{C}}{3 }$

(n>3 حيث n مرجح عدة نقط .( مرجح

تعريف :

لتكن $A_{n},....,A_{3},A_{2},A_{1},$ ، $n$ نقطة مرفقة بالمعاملات $\alpha _{n},...,\alpha _{3},\alpha _{2},\alpha _{1}$ على الترتيب حيث .

$\alpha _{1}+\alpha _{2}+\alpha _{3}+....+\alpha _{n}\neq 0$ نسمي مرجح النقط $A_{n},....,A_{3},A_{2},A_{1},$ مرفقة بالمعاملات $\alpha _{n},...,\alpha _{3},\alpha _{2},\alpha _{1}$ على الترتيب النقطة $G$ حيث :

$\alpha _{1}\overrightarrow{GA_{1}}+\alpha _{2}\overrightarrow{GA_{2}}+\alpha _{3} \overrightarrow{GA_{3}}+....+\alpha _{n}\overrightarrow{GA_{n}}= \vec{0}$ .

ملاحظة :

الخواص المعروفة في مرجح ثلاث نقط تبقى صحيحة .