ملخص الدرس / الثآنية ثانوي/رياضيات/الجبر و التحليل/الأشتقاقية

الدرس

عمليات على الدوال المشتقة

مشتقة مجموع دالتين :

مبرهنة :

$u$ و $v$ دالتان قابلتان للاشتقاق على مجال $D$ من $\mathbb{R}$ . الدالة $\left ( u+v \right )$ قابلة للاشتقاق على $D$ و دالتها المشتقة هي : ${\left ( u+v \right )}'={u}'+{v}'$

برهان :

من أجل كل عدد حقيقي $h$ يختلف عن $0$ . لدينا :

$\frac{\left ( u+v \right )\left ( x_{0}+h \right )-\left ( u+v \right )\left ( x_{0} \right )}{h} =\frac{u\left ( x_{0}+h \right )+v\left ( x_{0}+h \right )-u\left (x_{0} \right )-v\left ( x_{0} \right )}{h}$

$=\frac{u\left ( x_{0}+h \right )-u\left (x_{0} \right )}{h}+\frac{v\left ( x_{0}+h \right ) -v\left ( x_{0} \right )}{h}$

نضع $g_{1}\left ( h \right )=\frac{u\left ( x_{0}+h \right )-u\left (x_{0} \right )}{h}$ و $g_{2}\left ( h \right )=\frac{v\left ( x_{0}+h \right ) -v\left ( x_{0} \right )}{h}$ .

بما أن $u$ و $v$ قابلتان للاشتقاق على $D$ لدينا من أجل كل $x_{0}$ l من $D$ $\lim_{h\rightarrow 0}g_{1}\left ( h \right )={u}'\left ( x_{0} \right )$ و $\lim_{h\rightarrow 0}g_{2}\left ( h \right )={v}'\left ( x_{0} \right )$ .

و منه $\lim_{h\rightarrow 0}\frac{\left ( u+v \right )\left ( x_{0}+h \right )-\left ( u+v \right )\left ( x _{0}\right )}{h}={u}'\left ( x_{0} \right )+{v}'\left ( x_{0} \right )$ و منه صحة البرهان .

مشتقة جداء دالتين :

مبرهنة :

لتكن دالتان $u$ و $v$ قابلتان للاشتقاق على مجال $D$ ( $D$ هو مجال أو اتحاد مجالات من $\mathbb{R}$ ) . الدالة $\left (u.v \right )$ قابلة للاشتقاق على $D$ و دالتها المشتقة هي : ${\left ( u.v \right )}'={u}'.v+u.{v}'$ .

حالة خاصة :

الدالة $\left ( \lambda u \right )$ ( حيث $\lambda$ عدد حقيقي ) قابلة للاشتقاق على $D$ و دالتها المشتقة هي : ${\left ( \lambda u \right )}'=\lambda {u}'$

(عمليات على الدوال المشتقة(تابع

مشتقة مقلوب دالة :

مبرهنة :

$v$ دالة قابلة للاشتقاق على مجال $D$ من $\mathbb{R}$ و $v$ لا تنعدم على $D$ الدالة $\left ( \frac{1}{v} \right )$ قابلة للاشتقاق على $D$ و دالتها المشتقة هي : ${\left ( \frac{1}{v} \right )}'=-\frac{{v}'}{v^{2}}$ .

مشتقة نسبة دالتين :

مبرهنة :

لتكن دالتان $u$ و $v$ قابلتان للاشتقاق على مجال $D$ ( $D$ هو مجال أو اتحاد مجالات من $\mathbb{R}$ ) . و $v$ لا تنعدم على $D$ .

الدالة $\left ( \frac{u}{v} \right )$ قابلة للاشتقاق على $D$ و دالتها المشتقة هي : ${\left ( \frac{u}{v} \right )}'=\frac{{u}'v-u{v}'}{v^{2}}$ .

برهان :

نلاحظ أن $\left ( \frac{u}{v} \right )$ يكتب $u\times \frac{1}{v}$ و نطبق مبرهنة مشتقة مقلوب دالة و مبرهنة مشتقة جداء دالتين .

مشتقة الدالة $f:x \mapsto u\left ( ax+b \right )$ :

مبرهنة : (تقبل بدون برهان )

$u$ قابلة للاشتقاق على مجال $D$ من $\mathbb{R}$ . $a$ و $b$ عددان حقيقيان . $E$ مجموعة الاعداد الحقيقية $x$ حيث $ax+b$ ينتمي إلى $D$ . الدالة $f:x \mapsto u\left ( ax+b \right )$

قابلة للاشتقاق على $E$ و دالتها المشتقة ${f}'$ هي : ${f}':x \mapsto a{u}'\left ( ax+b \right )$ حيث ${u}'$ مشتقة الدالة $u$ على $D$ .

ملاحظة :

الدالة $f$ هي دالة مركبة من الدالة $k:x \mapsto ax+b$ متبوعة بالدالة $u$ أي $f=u\: o\: k$ .

جدول ملخص

تطبيقات الاشتقاقية

إتجاه تغير الدالة :

مبرهنة : (تقبل بدون برهان )

لتكن دالة $f$ معرفة و قابلة للاشتقاق على مجال $D_{f}$ و ${f}'$ دالتها المشتقة .

* إذا كانت ${f}'$ موجبة تماما ( يمكن أن تكون ${f}'$ معدومة من أجل قيم منعزلة من $D_{f}$ ) على المجال $D_{f}$ فإن الدالة $f$ متزايدة تماما على المجال $D_{f}$ .

* إذا كانت ${f}'$ سالبة تماما ( يمكن أن تكون ${f}'$ معدومة من أجل قيم منعزلة من $D_{f}$ ) على المجال $D_{f}$ فإن الدالة $f$ متناقصة تماما على المجال $D_{f}$ .

* إذا كانت ${f}'$ معدومة على المجال $D_{f}$ فإن الدالة $f$ ثابتة على المجال $D_{f}$ .

ملاحظة :

إذا كانت دالة $f$ إما متزايدة تماما و إما متناقصة تماما على مجال $D_{f}$ نقول أن الدالة $f$ رتيبة تماما على المجال $D_{f}$ .

القيم الحدية المحلية لدالة :

مبرهنة : (تقبل بدون برهان )

لتكن دالة $f$ معرفة و قابلة للاشتقاق على مجال $I$ و ${f}'$ دالتها المشتقة .

* إذا انعدمت الدالة المشتقة ${f}'$ عند قيمة $c$ من $I$ مغيرة إشارتها فإنه يوجد مجال مفتوح ${I}'$ محتوى في $I$ يشمل $c$ تقبل فيه $f$ قيمة حدية $f\left ( c \right )$ . تسمى $f\left ( c \right )$ قيمة حدية محلية .

ملاحظات :

* يمكن وجود عدة قيم حدية محلية على $I$ .

* إذا انعدمت الدالة المشتقة ${f}'$ عند قيمة $c$ من $I$ فإن الرسم البياني للدالة $f$ يقبل مماسا موازيا لحامل محور الفواصل عند النقطة التي فاصلتها $c$ .

تعليق :

في صورة شاشة الآلة $\mathrm{TI-83\: \: plus}$ المقابلة ، الرسم يمثل الدالة $f:x \mapsto x^3$ . مشتقتها ${f}':x \mapsto 3x^2$ الدالة ${f}'$ تنعدم عند $0$ و لاتغير الإشارة

و $f\left ( 0 \right )=0$

$0$ ليست قيمة حدية محلية للدالة $f$ .

Chargement en cours, Veuillez patientez...

حصر دالة

حصر دالة :

نتائج :

لتكن دالة $f$ معرفة و قابلة للاشتقاق على مجال $\left [ a;b \right ]$ و ${f}'$ دالتها المشتقة .

* إذا كانت الدالة $f$ متزايدة تماما على المجال $\left [ a;b \right ]$ فإن من أجل كل عدد حقيقي $x$ من المجال $\left [ a;b \right ]$ $f\left ( a \right )\leq f\left ( x \right )\leq f\left ( b \right )$ .

* إذا كانت الدالة $f$ متناقصة تماما على المجال $\left [ a;b \right ]$ فإن من أجل كل عدد حقيقي $x$ من المجال $\left [ a;b \right ]$ $f\left ( b \right )\leq f\left ( x \right )\leq f\left ( a \right )$ .

عنصر حاد من الأعلى - عنصر حاد من الأسفل :

تعريف :

لتكن دالة $f$ معرفة على مجال $D_{f}$ .

* يسمى عدد حقيقي $k$ عنصرا حادا من الأعلى $(Majorant)$ للدالة $f$ على المجال $D_{f}$ إذا و فقط إذا كان من أجل كل عدد حقيقي $x$ من المجال $D_{f}$ ، $f(x)\leq k$ .

* يسمى عدد حقيقي $k$ عنصرا حادا من الأسفل $(Minorant)$ للدالة $f$ على المجال $D_{f}$ إذا و فقط إذا كان من أجل كل عدد حقيقي $x$ من المجال $D_{f}$ ، $f(x)\geq k$ .

ملاحظة :

* القيمة الحدية الكبرى للدالة $f$ على المجال $D_{f}$ إن وجدت هي العنصر الحاد من الأعلى و هو أصغر العناصر الحادة من الأعلى .

* القيمة الحدية الصغرى للدالة $f$ على المجال $D_{f}$ إن وجدت هي العنصر الحاد من الأسفل و هو أكبر العناصر الحادة من الأسفل .

إتجاه تغير دالة

إتجاه تغير دالة :

مبرهنة (تقبل بدون برهان):

لتكن دالة $f$ معرفة وقابلة للإشتقاق على مجال $D_{f}$ و ${f}'$ دالتها المشتقة.

- إذا كانت ${f}'$ موجبة تماما (يمكن أن تكون ${f}'$ معدومة من أجل قيم منعزلة من $D_{f}$ ) على المجال $D_{f}$ فإن الدالة $f$ متزايدة تماماً على المجال $D_{f}$ .

- إذا كانت ${f}'$ سالبة تماماً (يمكن أن تكون ${f}'$ معدومة من أجل قيم منعزلة من $D_{f}$ ) على المجال $D_{f}$ فإن الدالة $f$ متناقصة تماماً على المجال $D_{f}$ .

- إذا كانت ${f}'$ معدومة على المجال $D_{f}$ فإن الدالة $f$ ثابتة على المجال $D_{f}$

ملاحظة :

إذا كانت دالة $f$ إما متزايدة تماماً وإما متناقصة تماماً على مجال $D_{f}$ نقول أن الدالة $f$ رتيبة تماماً على المجال $D_{f}$ .

مثال : لتكن الدالة $f$ المعرفة على $\mathbb{R}$ كما يلي : $f:x \mapsto -x^3 + 2$ .

الدالة $f$ قابلة للإشتقاق على $\mathbb{R}$ ودالتها المشتقة ${f}'$ حيث : ${f}' : x \mapsto -3x^2$ .

الدالة $f$ سالبة تماماً على $\mathbb{R}^{\circ}$ وتنعدم في النقطة المعزولة $0$ إذن الدالة $f$ متناقصة تماماً على $\mathbb{R}$ .

القيم الحدية المحلية لدالة

القيم الحدية المحلية لدالة :

مبرهنة (تقبل بدون برهان) :

لتكن دالة $f$ معرفة وقابلة للإشتقاق على مجال $I$ و ${f}'$ دالتها المشتقة.

- إذا انعدمت الدالة المشتقة ${f}'$ عند قيمة $c$ من $I$ مغيرة إشارتها فإنه يوجد مجال مفتوح ${I}'$ محتوى في $I$ يشمل $c$ تقبل فيه $f$ قيمة حدية $f(c)$ ، تسمى $f(c)$ قيمة حدية محلية.

ملاحظات :

- يمكن وجود عدة قيم حدية محلية على $I$ .

- إذا انعدمت الدالة المشتقة ${f}'$ عند قيمة $c$ من $I$ فإن الرسم البياني للدالة $f$ يقبل مماسا موازيا لحامل محور الفواصل عند النقطة التي فاصلتها $c$ .

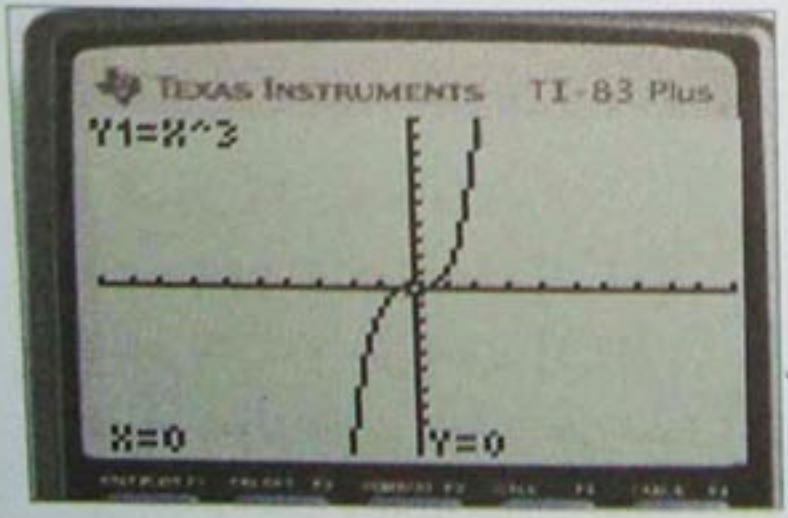
تعليق :

في صورة شاشة الآلة $TI-83 Plus$ التالية، الرسم يمثل الدالة $f: x \mapsto x^3$ ، مشتقتها ${f}':x \mapsto 3x^2$ ، الدالة ${f}'$ تنعدم عند $0$ ولا تغير الإشارة، و $f(0)=0$ .

$0$ ليست قيمة حدية محلية للدالة $f$ .

حصر دالة

حصر دالة :

نتائج :

لتكن دالة $f$ معرفة وقابلة للإشتقاق على مجال $\left [ a,b \right ]$ و ${f}'$ دالتها المشتقة.

- إذا كانت الدالة $f$ متزايدة تماماً على المجال $\left [ a,b \right ]$ فإن من أجل كل عدد حقيقي $x$ من المجال $\left [ a,b \right ]$ : ${\color{Red} f(a) \leq f(x) \leq f(b)}$ .

- إذا كانت الدالة $f$ متناقصة نماماً على المجال $\left [ a,b \right ]$ فإن من أجل كل عدد حقيقي $x$ من المجال $\left [ a,b \right ]$ : ${\color{Red} f(b) \leq f(x) \leq f(a)}$ .

مثال :

لتكن الدالة $f$ المعرفة على $\left [ -3,1 \right ]$ كما يلي : $f:x \mapsto x^2 +2x-3$ .

- الدالة $f$ قابلة للإشتقاق على $\mathbb{R}$ ودالتها المشتقة ${f}'$ هي : ${f}' : x \mapsto 2x + 2$ .

- الدالة ${f}'$ سالبة تماماً على $\left [ -3,-1 \right ]$ و ${f}'(-1) = 0$ إذن الدالة $f$ متناقصة تماماً على المجال $\left [ - 3,-1 \right [$ .

- الدالة ${f}'$ موجبة تماماً على $\left ]-1,1 \right ]$ إذن الدالة $f$ متزايدة تماماً على المجال $\left ]-1,1 \right ]$ .

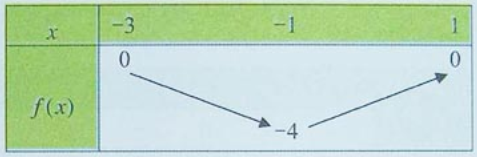
جدول التغيرات في الصورة المرفقة

من أجل كل $x$ من المجال $\left [ -3,-1 \right ]$ ، $f(-1)\leq f(x)\leq f(-3)$ أي $-4 \leqslant f(x)\leq 0$ .

من أجل كل $x$ من المجال $\left [ -1,1 \right ]$ ، $f(-1)\leq f(x)\leq f(1)$ أي $-4 \leq f(x)\leq 0$ .

عنصر حاد من الأعلى - عنصر حاد من الأسفل

عنصر حاد من الأعلى - عنصر حاد من الأسفل :

تعريف :

لتكن دالة $f$ معرفة على مجال $D_{f}$ .

- يسمى عدد حقيقي $k$ عنصراً حاداً من الأعلى $(Majorant)$ للدالة $f$ على المجال $D_{f}$ إذا وفقط إذا كان من أجل كل عدد حقيقي $x$ من المجال $D_{f}$ ، ${\color{Red} f(x)\leq k}$ .

- يسمى عدد حقيقي $k$ عنصراً حاداً من الأسفل $(Minorant)$ للدالة $f$ على المجال $D_{f}$ إذا وفقط إذا كان من أجل كل عدد حقيقي $x$ من المجال $D_{f}$ ، ${\color{Red} f(x)\geq k}$ .

بالنسبة للمثال السابق الدالة $f$ المعرفة على $\left [ -3,1 \right ]$ كما يلي : $f:x \mapsto x^2 +2x-3$ .

0 عنصر حاد من الأعلى و $-4$ عنصر حاد من الأسفل.

ملاحظة :

- القيمة الحدية الكبرى للدالة $f$ على $D_{f}$ إن وجدت هي العنصر الحاد من الأعلى وهو أصغر العناصر الحادة من الأعلى.

- القيمة الحدية الصغرى للدالة $f$ على $D_{f}$ إن وجدت هي العنصر الحاد من الأسفل وهو أكبر العناصر الحادة من الأسفل.

ملخص الدرس / الثآنية ثانوي/رياضيات/الجبر و التحليل/الأشتقاقية

الدرس

عمليات على الدوال المشتقة

مشتقة مجموع دالتين :

مبرهنة :

برهان :

مشتقة جداء دالتين :

مبرهنة :

حالة خاصة :

(عمليات على الدوال المشتقة(تابع

مشتقة مقلوب دالة :

مبرهنة :

مشتقة نسبة دالتين :

مبرهنة :

برهان :

مشتقة الدالة :

مبرهنة : (تقبل بدون برهان )

ملاحظة :

جدول ملخص

تطبيقات الاشتقاقية

إتجاه تغير الدالة :

مبرهنة : (تقبل بدون برهان )

ملاحظة :

القيم الحدية المحلية لدالة :

مبرهنة : (تقبل بدون برهان )

ملاحظات :

تعليق :

حصر دالة

حصر دالة :

نتائج :

عنصر حاد من الأعلى - عنصر حاد من الأسفل :

تعريف :

ملاحظة :

إتجاه تغير دالة

إتجاه تغير دالة :

القيم الحدية المحلية لدالة

القيم الحدية المحلية لدالة :

حصر دالة

حصر دالة :

عنصر حاد من الأعلى - عنصر حاد من الأسفل

عنصر حاد من الأعلى - عنصر حاد من الأسفل :

مشتقة الدالة $f:x \mapsto u\left ( ax+b \right )$ :