ملخص الدرس / الأولى متوسط/رياضيات/الأنشطة الهندسية/التناظر المحوري
الملخص
من الأستاذ(ة) ELBEY Mouloudالتناظر المحوري
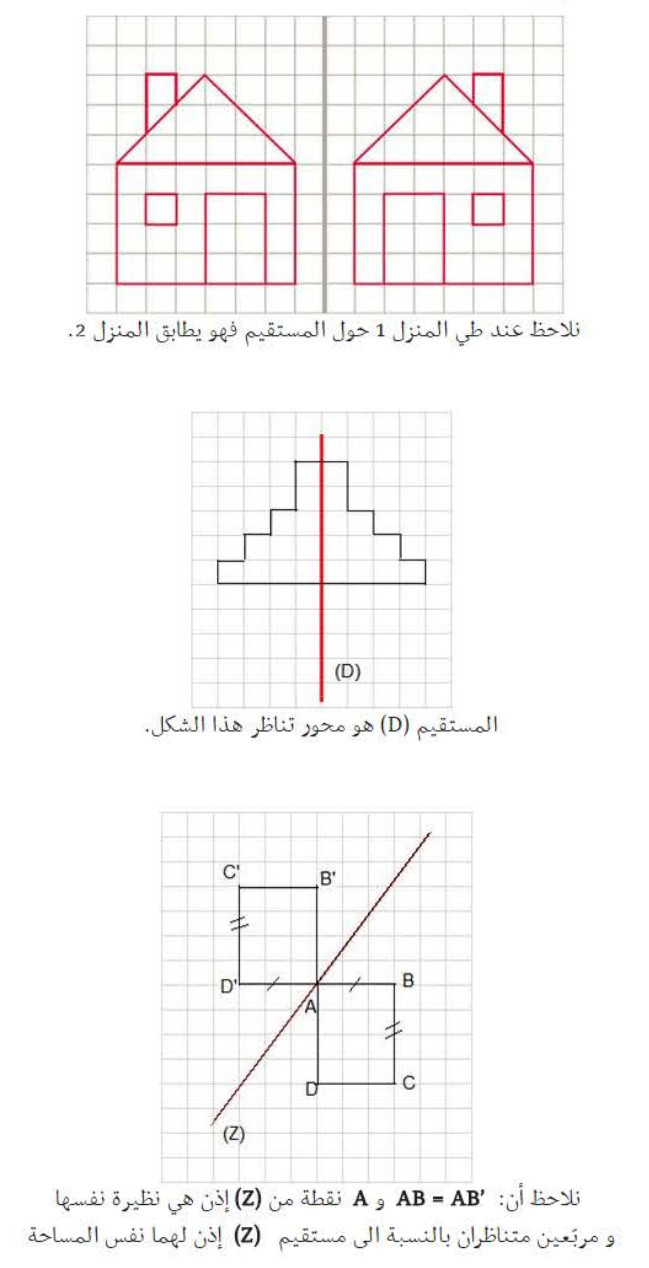
1- التناظر المحوري:
تعريف:
- نقول عن شكلين أنهما متناظران بالنسبة إلى مستقيم إذا تطابقا عند استخدام الطي حول المستقيم (الشكل الأول).
- إذا كان مستقيم محور تناظر شكل ما معناه أن هذا الشكل هو نظير نفسه بالنسبة إلى المستقيم (الشكل الثاني).
- التناظر المحوري يحفظ المساحات، المسافات، وأقياس الزوايا (الشكل الثالث).
نظير نقطة بالنسبة إلى مستقيم
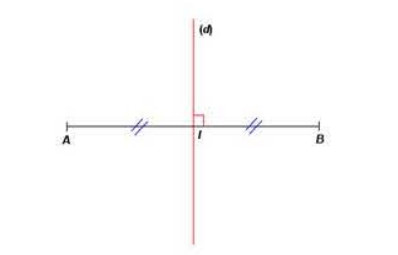
2- نظير نقطة بالنسبة إلى مستقيم:
تذكير:
- تكون نقطتان و
مختلفتان متناظرتان بالنسبة إلى مستقيم
إذا كان المستقيم
محور القطعة
.
- كل نقطة من المستقيم هي نظيرة نفسها بالنسبة إلى هذا المستقيم.
محاور تناظر الأشكال المألوفة
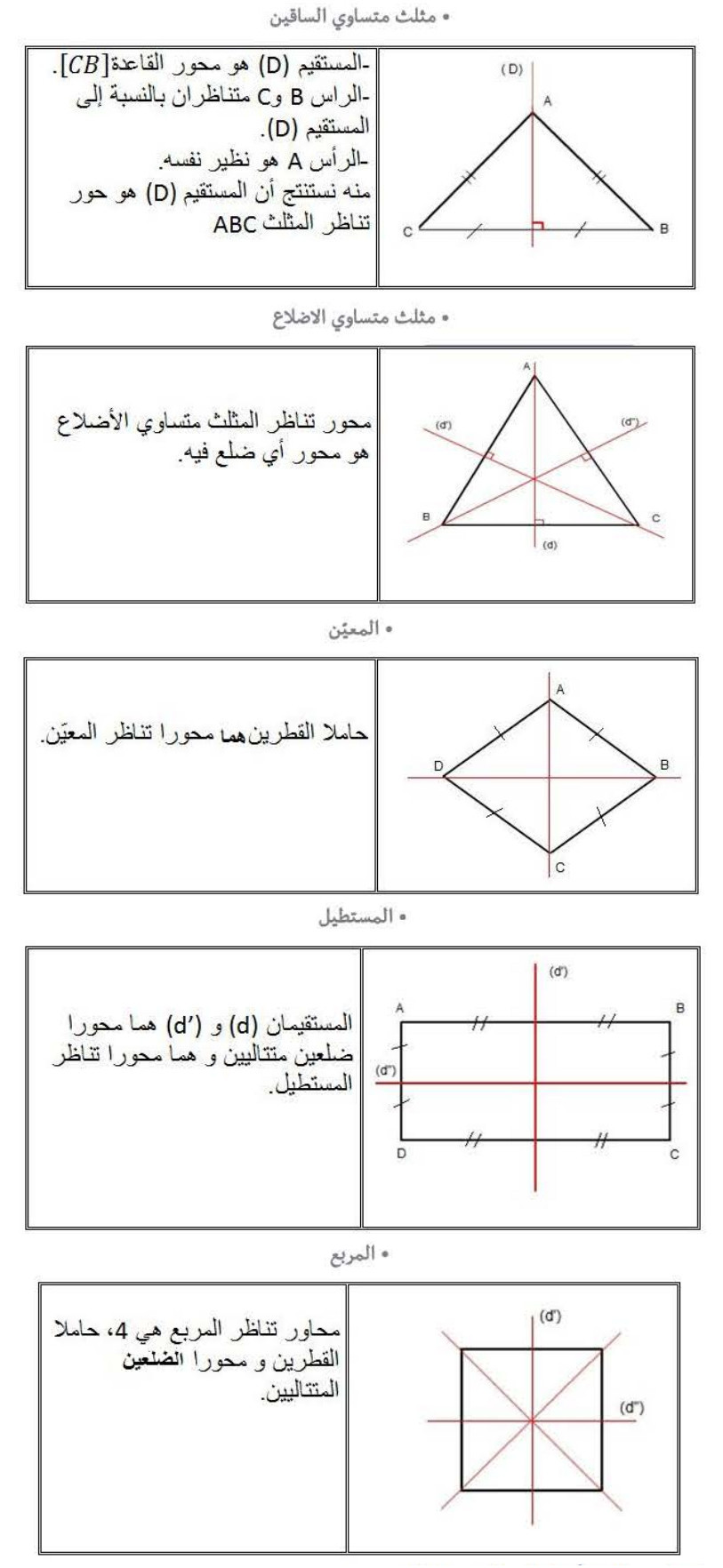
3- محاور تناظر الأشكال المألوفة:
إنشاء نظائر أشكال بالنسبة إلى مستقيم
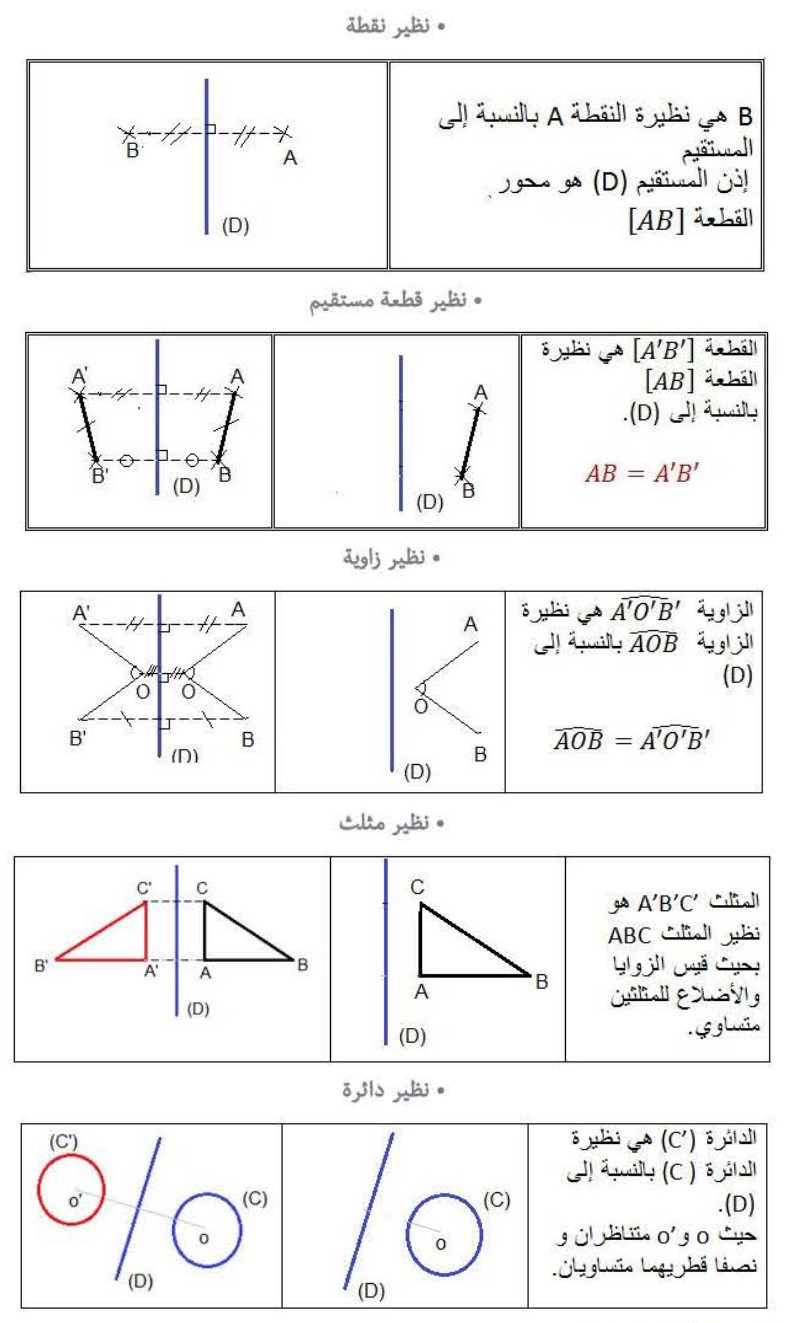
4- إنشاء نظائر أشكال بالنسبة إلى مستقيم:
محور قطعة مستقيم
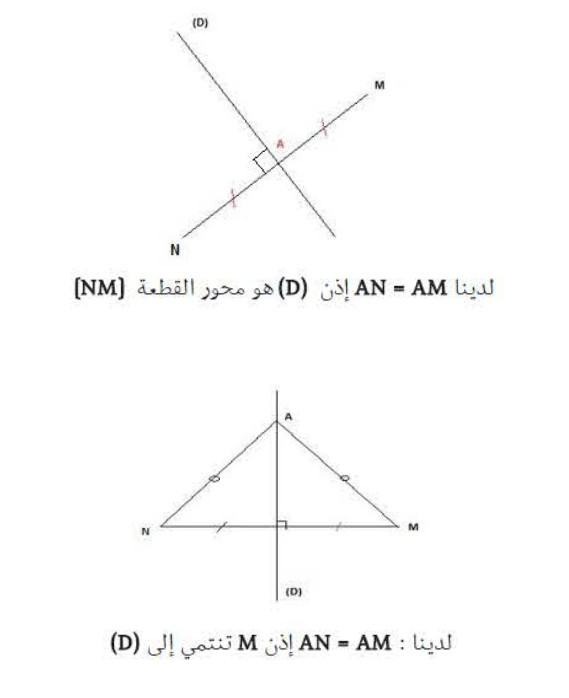
5- محور قطعة مستقيم:
- محور قطعة مستقيم هو المستقيم العمودي في منتصفها (الشكل الأول).
- إذا كانت نقطة متساوية المسافة عن بعدي قطعة مستقيمة إذن هذه النقطة تنتمي إلى محور هذه القطعة (الشكل الثاني).
منصف زاوية
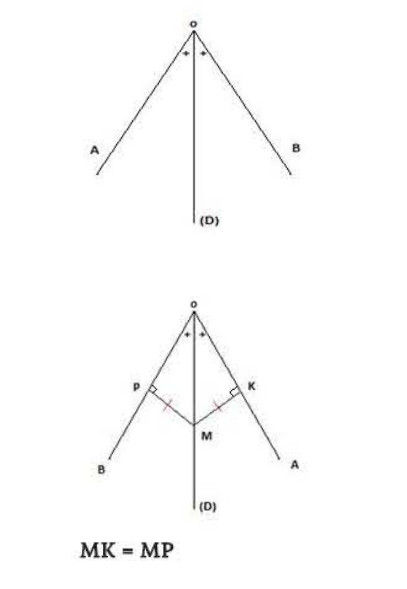
6- منصف زاوية:
تعريف:
منصف الزاوية هو نصف المستقيم الذي مبدؤه هو رأس الزاوية والذي يقسم الزاوية إلى زاويتين متقايستين حيث يسمى منصف الزاوية محور تناظر لهذه الزاوية (الشكل الأول).
ملاحظة:
كل نقطة تنتمي إلى منصف زاوية تكون متساوية المسافة عن ضلعي هذه الزاوية (الشكل الثاني).
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :