ملخص الدرس / الأولى متوسط/رياضيات/الأنشطة الهندسية/الأشكال المستوية

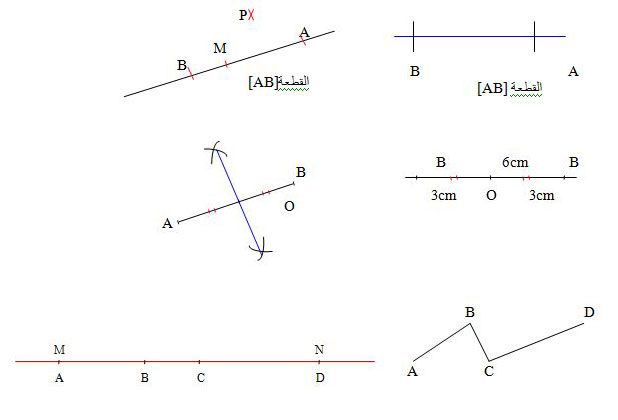
تعريف :

 النقط المحصورة بين النقطتين   تمثل قطعة مستقيم طرفاها النقطتان    يرمز لهذه القطعة بالرمز :  أو 

الانتماء و عدم الانتماء :

لاحظ الشكل الآتي :

نقطة من القطعة   نقول أن  النقطة   تنتمي إلى القطعة , و نكتب : 

  نقطة ليست من نقط القطعة   نقول أن النقطة   لا تنتمي إلى القطعة , و نكتب : 

منتصف قطعة مستقيم :

منتصف قطعة مستقيم هو قطعة من هذه القطعة تقسمها إلى قطعتين لهما نفس الطول

استخدام المدور و المسطرة لإنشاء منتصف قطعة مستقيم :

استخدام المدور و المسطرة لإنشاء منتصف القطعة

استخدام المدور و المسطرة لإنشاء قطعة مستقيم طولها يساوي مجموع أطوال قطع مستقيم معطاة :

لاحظ الشكل : 

أنشاء    بحيث : 

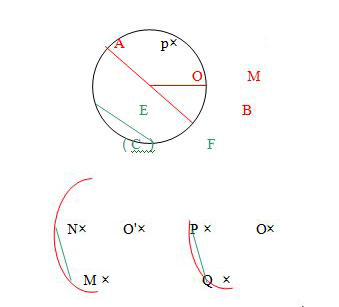
الدائرة :

الشكل المقابل يمثل دائرة   مركزها  ونصف قطرها   هي كل النقط التي تبعد عن المركز بنفس المسافة 

يرمز للدائرة بحرف كبير مثل                        

القطر : 

هو قطعة مستقيم تشمل المركز و طرفاها نقطتان من     يمثل قطر الدائرة     

نصف القطر :

  أنصاف القطر حيث  

الوتر : 

 هو قطعة مستقيم طرفاها نقطتان من   ولا يشمل المركز: مثال     وتر للدائرة   

داخل وخارج دائرة :

لدينا :

 فالنقطة داخل الدائرة

  فالنقطة   خارج الدائرة

كيفية إنشاء قوس يقايس قوسا أخر  :

  قوسا من دائرة مركزها   , أنشئ قوسا   يقايس 

• أعين نقطة 
• أرسم دائرة مركزها ونصف قطرها     
• أعين نقطة   ثم نقطة   بحيث    :   

الزاوية :

الشكل المقابل يمثل زاوية                                            

   رأس الزاوية 

   ضلعا الزاوية

وحدة قياس الزاوية هي الدرجة ( ° )

المنقلة هي أداة قياس الزوايا و هي مدرجة من °0 إلى °180

أنواع الزوايا :

الزاويتان المتتامتان  :  هما زاويتان مجموع قيسيهما يساوي °90

الزاويتان المتكاملتان :  هما زاويتان مجموع قيسيهما يساوي °180 

المضلعات الخاصة :

1) المثلث المتساوي الساقين :    

هو مثلث له ضلعان متقايسان   شكل (1) 

2) المثلث المتقايس الأضلاع :  

 هو مثلث أضلاعه متقايسة   شكل (2) 

3) المثلث القائم :

هو مثلث إحدى زواياه قائمة   شكل (3)

شبه المنحرف :                                                         

هو رباعي فيه ضلعان متقابلان حاملاهما متوازيان و الضلعان  الآخران حاملاهما غير متوازيان                                                                                                      

أشباه المنحرف الخاصة :

1) شبه المنحرف القائم :

هو شبه منحرف أحد ضلعيه الجانبيين عمودي على القاعدتين                                                                  

   ,    =  ° 90  ,     =  ° 90

2) شبه المنحرف المتساوي الساقين :

هو شبه منحرف ضلعاه الجانبيان متقايسان  

      ,     ,  

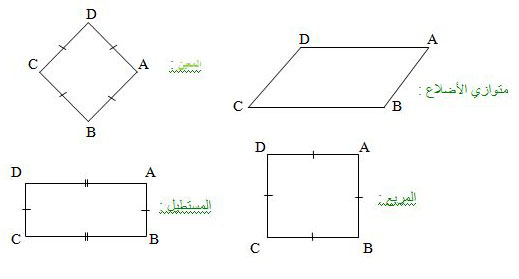
متوازي الأضلاع :

متوازي الأضلاع هو رباعي فيه كل ضلعين متعامدين حاملاهما متوازيان

   ,     

   ,  و                                                                    

متوازيات الأضلاع الخاصة :

المعين :

المعين هو متوازي أضلاع له ضلعان متتاليان متقايسان 

المستطيل :

المستطيل هو متوازي أضلاع إحدى زوياه قائمة

   ,  و    

 °90               

المربع :

المربع هو متوازي أضلاع له ضلعان متتاليان متقايسان و إحدى زواياه قائمة

°90