ملخص الدرس / الثانية متوسط/رياضيات/الأنشطة العددية/العمليات على الكسور

الملخص

من الأستاذ(ة) ELBEY Mouloud

العمليات على الكسور

1- العمليات على الكسور:

عناصر الدرس:

- القسمة على عدد عشري غير معدوم - القيم المقربة - حصر عدد عشري.

- القيم المقربة.

- ضرب كسرين.

- مقارنة كسرين.

- جمع وطرح كسري.

أ) القسمة على عدد عشري غير معدوم:

قاعدة:

من أجل حساب حاصل قسمة عدد على عدد عشري غير معدوم نحوله إلى حاصل قسمة مقامه عدد طبيعي ويتم ذلك بضرب البسط والمقام في 10 أو 100 أو 1000.

مثال:

قسمة العدد العشري 9,3 على 0,2:

$9,3 \div 0,2 = \frac{9,3}{0,2} = \frac{9,3 \ast 10}{0,2 \ast 10} = \frac{93}{2} = 46,5$

مثال:

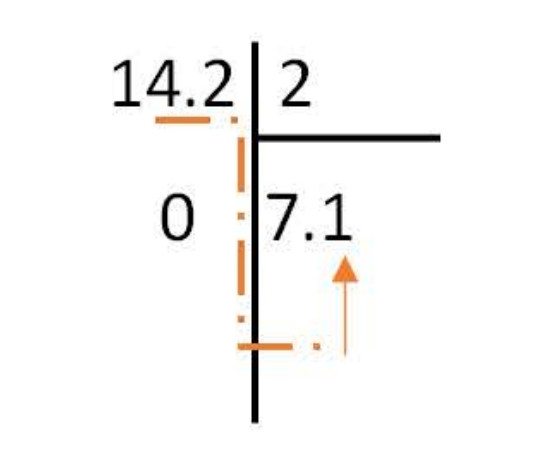
قسمة العدد العشري 1,42 على 0,2:

$1,42 \div 0,2 = \frac{1,42}{0,2} = \frac{1,42\ast 10}{0,2 \ast 10} = \frac{14,2}{2} = 7,1$

طريقة قسمة 1,42 على 0,2 عمليا:

نضرب كل من 0,2 و 1,42 في 10 ونجري القسمة كما في الشكل.

فيديوا تعليمي لتمارين حول الدرس:

القيمة المقربة

ب) القيمة المقربة:

قاعدة (1):

عندما نجري قسمة عدد على عدد عشري غير معدوم فنجد أن القسمة لا تنتهي والحاصل غير عشري يلزمنا إعطاء قيمة مقربة بالنقصان أو الزيادة إلى الوحدة أو إلى $\frac{1}{10}$ أو إلى $\frac{1}{100}$ أو إلى $\frac{1}{1000}$ .

مثال:

قسمة 2,31 على 1,7.

$2,31 \div 1,7 = \frac{2,31}{1,7} = \frac{2,31 \ast 10}{1,7 \ast 10} = \frac{23,1}{17} = 1,35882...$

- القيمة المقربة إلى الوحدة بالنقصان هي 1 وبالزيادة هي $(1+1)$ أي ما يعادل 2.

- القيمة المقربة إلى $\frac{1}{10}$ بالنقصان هي 1,3 وبالزيادة هي $(1,3 + 0,1)$ أي ما يعادل 1,4.

- القيمة المقربة إلى $\frac{1}{100}$ بالنقصان هي 1,35 وبالزيادة هي $(1,35 + 0,01)$ أي 1,36.

- القيمة المقربة إلى $\frac{1}{1000}$ بالنقصان هي 1,358 وبالزيادة هي $(1,358 + 0,001)$ أي 1,359.

قاعدة (2):

حصر حاصل قسمة عدد على عدد عشري:

- نجري عملية القسمة كما في السابق.

- نعطي للحاصل القيم المقربة إلى الوحدة وإلى $\frac{1}{1000} ; \frac{1}{100} ; \frac{1}{10}$ : بالزيادة و النقصان.

- وأخيرا نحصر الحاصل.

مثال:

نأخذ المثال السابق: أوجد حصور حاصل قسمة 2,31 على 1,7 وجدنا القيم المقربة كاالتالي:

القيم المقربة بالنقصان إلى الوحدة وإلى $\frac{1}{10}$ ، $\frac{1}{100}$ ، $\frac{1}{1000}$ هي على التوالي : 2، 1,4، 1,36، 1,359.

$1 < \frac{2,31}{1,7} < 2$ حصر العدد إلى الوحدة.

$1,3 < \frac{2,31}{1,7} < 1,4$ حصر العدد إلى $\frac{1}{10}$ أي 0,1.

$1,35 < \frac{2,31}{1,7} < 1,36$ حصر العدد إلى $\frac{1}{100}$ أي 0,01.

فيديوا تعليمي حول الدرس:

ضرب كسرين

2- ضرب كسرين:

قاعدة:

لضرب الكسرين $\frac{a}{b}$ و $\frac{c}{d}$ نضرب البسط في البسط والمقام في المقام كما يلي:

$\frac{a}{b} \ast \frac{c}{d} = \frac{a\ast c}{b\ast d}$ حيث : $b \neq 0$ و $d \neq 0$ .

مثال:

- حساب $\frac{5}{3} \ast \frac{7}{2}$ :

$\frac{5}{3} \ast \frac{7}{2} = \frac{5\ast 7}{3\ast 2} = \frac{35}{6}$

مثال:

حساب $\frac{3,4}{5} \ast 2,1$

$\frac{3,4}{5} \ast 2,1 = \frac{3,4 \ast 2,1}{5} = \frac{7,14}{5}$

فيديوا تعليمي للإختبار الاول للفصل الأول:

مقارنة كسرين

أ) مقارنة كسرين:

- مقارنة كسرين لهما نفس المقام:

قاعدة:

إذا كان كسرين لهما نفس المقام فإن الكسر الأكبر هو الذي له أكبر بسط.

مثال:

مقارنة الكسرين $\frac{15}{4}$ و $\frac{3}{4}$ .

لدينا: $15 > 3$

إذن نستنتج أن $\frac{15}{4} > \frac{3}{4}$

- مقارنة كسرين مقام أحدهما مضاعف الآخر:

قاعدة:

نضرب بسط ومقام أحد الكسرين في عدد حتى يصبح للكسرين نفس المقام ثم نقارن.

مثال:

مقارنة الكسرين $\frac{7}{6}$ و $\frac{2}{3}$

نوحد المقامات ليصبح للكسرين نفس المقام.

$\frac{2}{3} = \frac{2\ast 2}{3\ast 2} = \frac{4}{6}$

أصبح لهما نفس المقام $\frac{4}{6}$ ، $\frac{7}{6}$ .

$\frac{7}{6} > \frac{4}{6}$

إذن:

$\frac{7}{6} > \frac{2}{3}$

- مقارنة كسر والعدد 1:

قاعدة:

يكون $\frac{a}{b} < 1$ إذا كان $b > a$ .

يكون $\frac{a}{b} > 1$ إذا كان $b < a$

حيث $b$ لا يساوي الصفر.

مثال:

$\frac{9}{3} > 1$ لأن $9 > 3$

$\frac{4}{7} < 1$ لأن $7 > 4$ .

فيديوا تعليمي حول الدرس:

جمع وطرح كسرين

ب- جمع وطرح كسرين:

- الكسران لهما نفس المقام:

قاعدة:

لجمع أو طرح كسرين لهما نفس المقام نجمع البسطين ونحتفظ بنفس المقام، في حالة الجمع: $\frac{a}{b} + \frac{c}{b} = \frac{a+c}{b}$ .

في حالة الطرح $\frac{a}{b} - \frac{c}{b} = \frac{a-c}{b}$ حيث $a$ أكبر أو يساوي $c$ .

مثال:

$\frac{3}{5} + \frac{10}{5} = \frac{3+10}{5} = \frac{13}{5}$

- مقام أحد الكسرين مضاعف للآخر:

قاعدة:

لجمع أو طرح كسرين مقام أحدهما مضاعف للآخر نتبع الخطوتين التاليتين:

نكتب الكسرين بنفس المقام أي نوحد المقامات.

نجمع أو نطرح البسطين ونحتفظ بنفس المقام.

مثال:

$\frac{7}{6} + \frac{5}{2} = \frac{7}{6} + \frac{5\ast 3}{2\ast 3} = \frac{7}{6} + \frac{15}{6} = \frac{7+15}{6} = \frac{22}{6}$

فيديوا تعليمي حول الدرس:

إستعمال الآلة الحاسبة

ت) إستعمال الآلة الحاسبة:

قاعدة:

لإجراء حسابات على الكسور بحاسبة يمكن استعمال أحد المسلمسين $ab/c$ أو $/$ حسب نوع الحاسبة.

مثال:

لننجز العملية باستعمال الحاسبة:

$\frac{4}{8} + \frac{1}{5} = \frac{7}{10}$