ملخص الدرس / الثانية متوسط/رياضيات/الأنشطة الهندسية/إنشاء أشكال هندسية
الملخص
من الأستاذ(ة) ELBEY Mouloudإنشاء أشكال هندسية
إنشاء أشكال هندسية:
عناصر الدرس:
- المستقيمان المتوازيان والمستقيمان المتعامدان.
- محور قطعة مستقيم - منصف زاوية.
- مثلثات خاصة.
- المستطيل المربع، المعين، الدائرة و قوس الدائرة.
1) المستقيمان المتوازيان والمستقيمان المتعامدان:
تعريف (1):
يكون مستقيمان متوازيان إذا كانا لا يشتركان في أي نقطة.
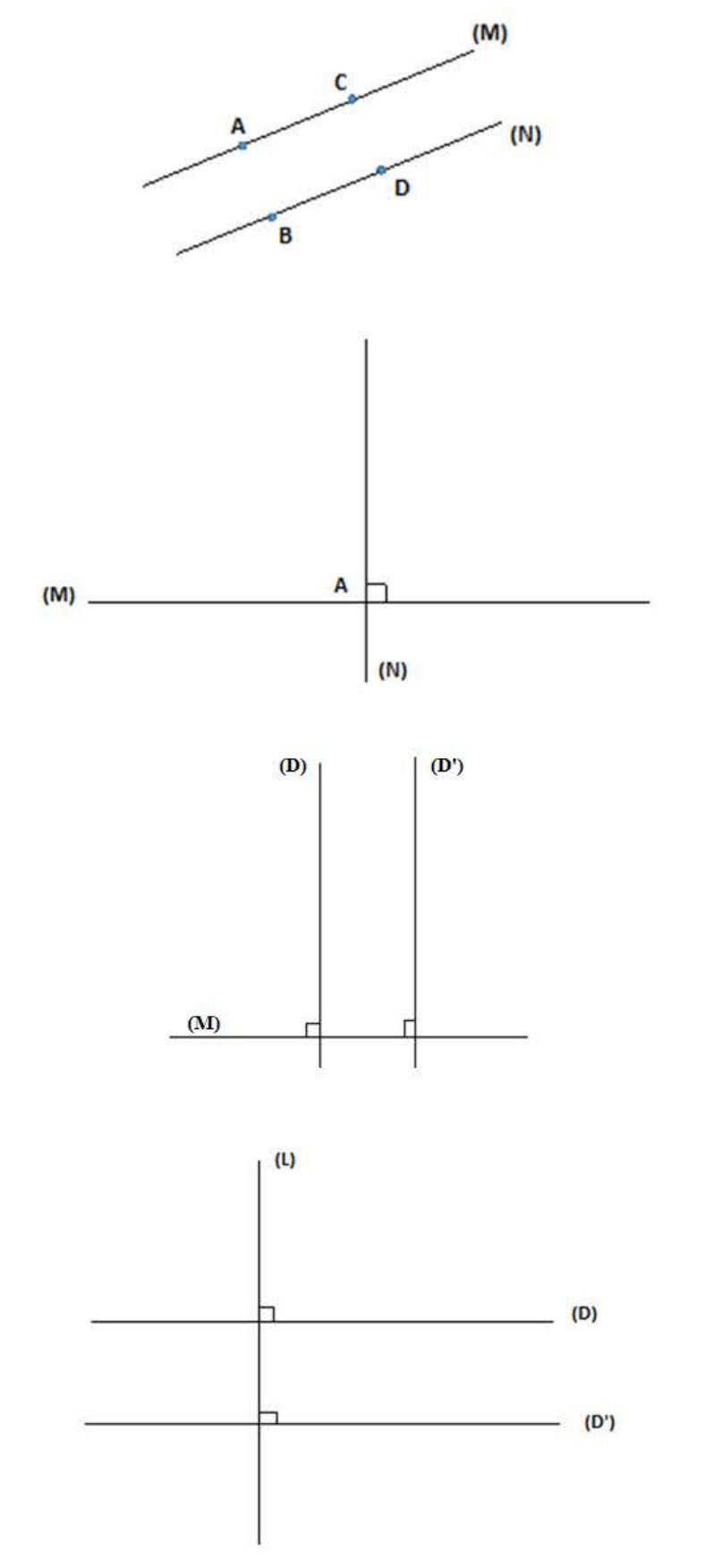
مثال (لاحظ الشكل 01):
المستقيم يوازي
.
ونكتب :
تعريف (2):
المستقيمان المتعامدان هما المستقيمان المتقاطعان اللذان يحددان زاوية قائمة، حيث نرمز للتعامد بالرمز .
مثال (لاحظ الشكل 02):
و
متعامدان ومتقاطعان في النقطة
.
إذن :
.
ونقول أن المستقيم عمودي على المستقيم
في النقطة
.
خاصية (1):
إذا كان مستقيمان متوازيان فكل مستقيم عمودي على أحدهما يكون عموديا على الآخر.
مثال (لاحظ الشكل 03):
لدينا: و
.
إذن :
خاصية (2):
إذا كان مستقيمان عموديان على مستقيم واحد إذن هما متوازيان.
مثال (لاحظ الشكل 04):
لدينا : و
.
إذن :
ملاحظة :
لاحظ الأشكال بالتتالي.
فيديوا تعليمي لتمارين حول الدرس:
محور قطعة مستقيم
2) محور قطعة مستقيم - منصف زاوية:
أ) محور قطعة مستقيم:
تعريف:
محور قطعة مستقيمة هو ذلك المستقيم العمودي على منتصف هذه القطعة.
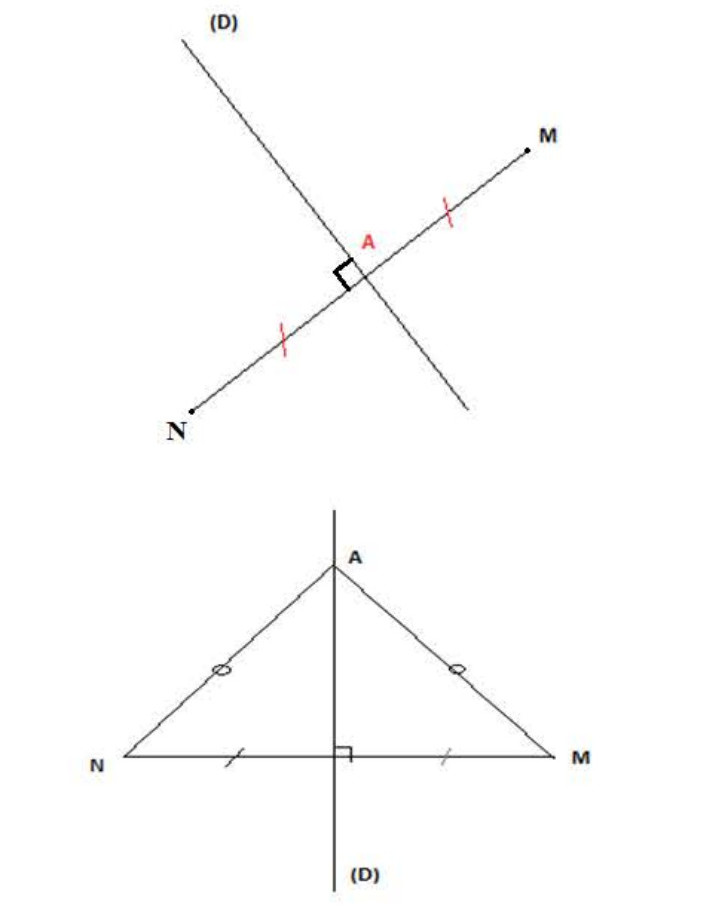
مثال (لاحظ الشكل 01):
لدينا: في النقطة
و
.
إذن نقول : محور للطعة
.
تذكير:
- محور قطعة مستقيم هو محور تناظر لها.
- أي نقطة من مجور قطعة مستقيم لها نفس البعد عن طرفي هذه القطعة.
محور
و
نقطعة من
.
إذن : .
(لاحظ الشكل 03).
منصف زاوية
ب) منصف زاوية:
تعريف:
منصف زاوية هو المستقيم الذي يقسم هذه الزاوية إلى زاويتين متقايستين.
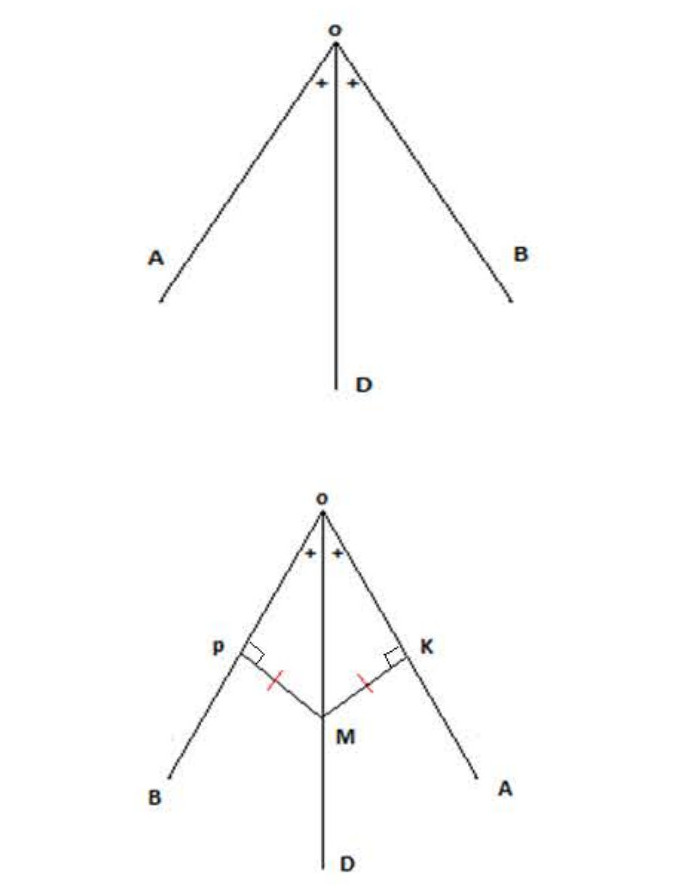
مثال (لاحظ الشكل 01):
هو منصف الزاوية
.
إذن: .
تذكير:
- منصف الزاوية هو محور تناظر لها.
- كل نقطة تنتمي إلى منصف الزاوية تكون متساوية المسافة عن ضلعي هذه الزاوية.
منصف الزاوية هو المستقيم
و
نقطة من
.
إذن : .
* (لاحظ الشكل 02).
مثلثات خاصة
3) مثلثات خاصة:
تعريف: المثلث المتساوي الساقين له ضلعين لهما نفس الطول.
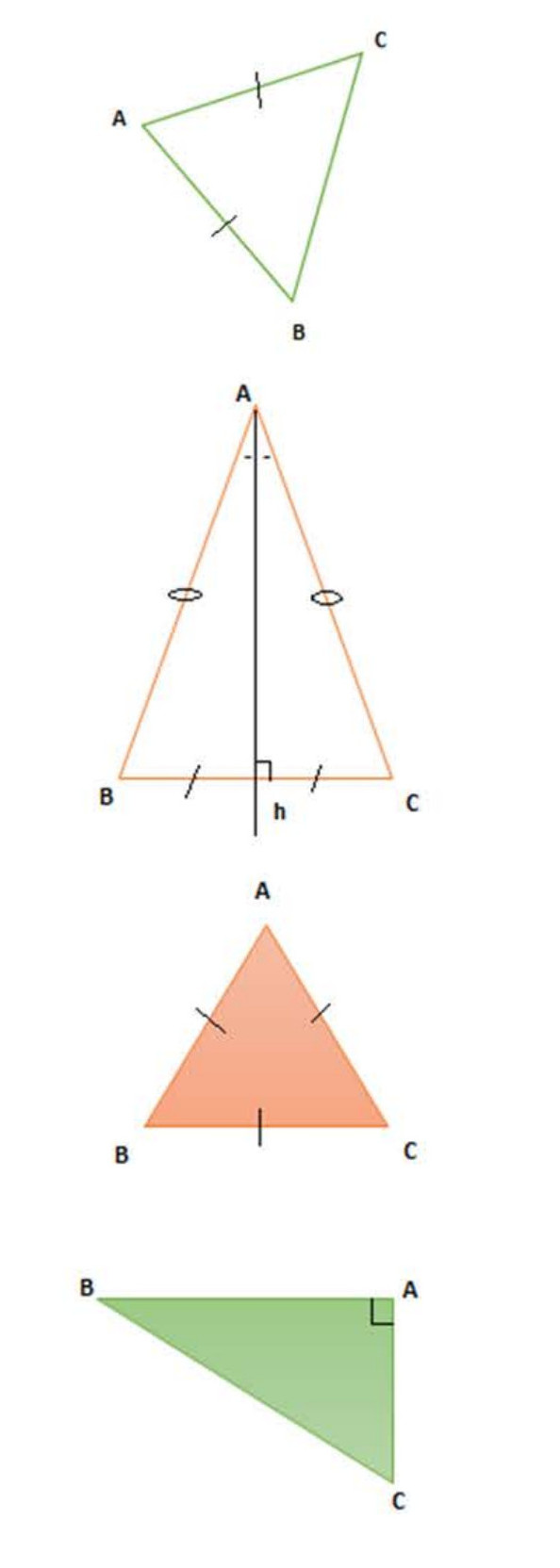
مثال (لاحظ الشكل 01):
لدينا: .
إذن المثلث متساوي الساقين.
تذكير:
- محور تناظر قاعدة مثلث متساوي الساقين هو نفسه محور تناظر هذا المثلث.
- محور تناظر قاعدة مثلث متساوي الساقين هو منصف زاوية الرأس الأساسي للمثلث .
* (لاحظ الشكل 02).
تعريف:
المثلث المتساوي الأضلاع هو مثلث طول أضلاعه الثلاثة متساوية أي لهم نفس الطول.
تذكير:
المثلث المتقايس الأضلاع هو مثلث أضلاعه لها نفس الطول.
الرأس الأساسي لمثلث متقايس الأضلاع هو أحد رؤوسه الثلاثة.
* (لاحظ الشكل 03).
تعريف:
المثلث القائم هو المثلث الذي له زاوية قائمة °
* (لاحظ الشكل 04).
المستطيل
4) المستطيل، المربع والدائرة.
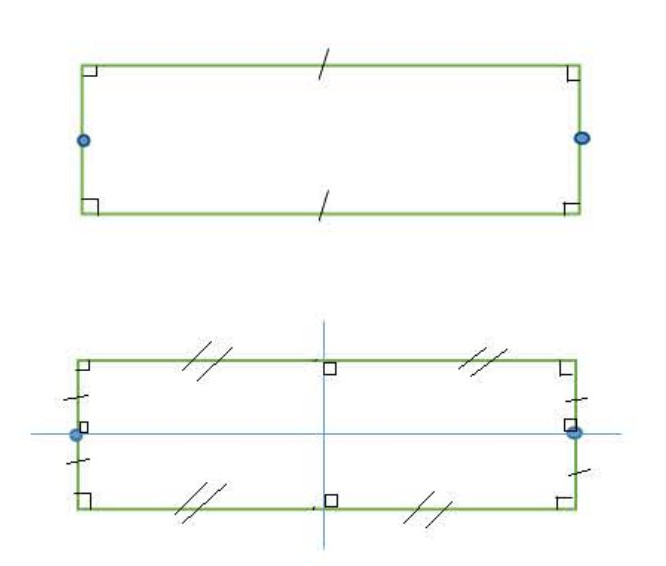
أ) المستطيل:
تعريف:
المستطيل هو شكل رباعي له ضلعين متقابلين متقايسان وله أربع زوايا قائمة (لاحظ الشكل 01).
تذكير:
محور كل ضلعين متقابلين من المستطيل يمثلان محورا تناظر لهذا المستطيل (لاحظ الشكل 02).
المربع
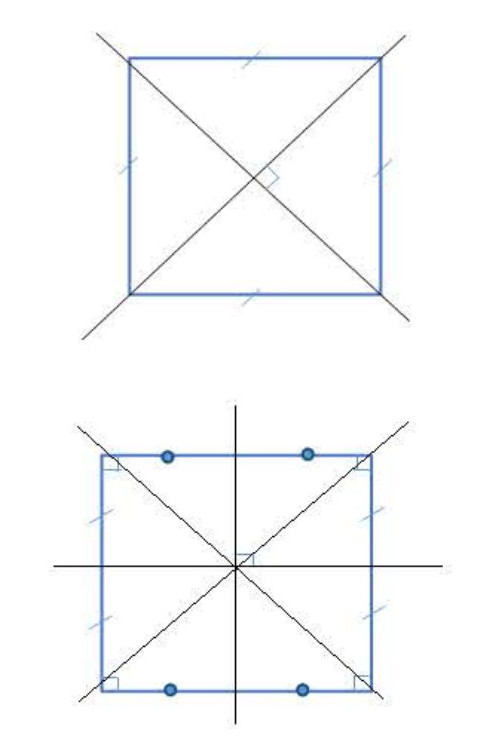
ب) المربع:
تعريف:
المربع هو شكل رباعي أضلاعه الأربعة متقايسة وله أربع زوايا قائمة (لاحظ الشكل 01).
تذكير:
- محور كل ضلعين متقابلين في المربع يمثلان محورا تناظر لهذا المربع.
- قطرا المربع متعامدان وكل منهما هو محور تناظر له (لاحظ الشكل 02).
فيديوا تعليمي حول الدرس:
المعين
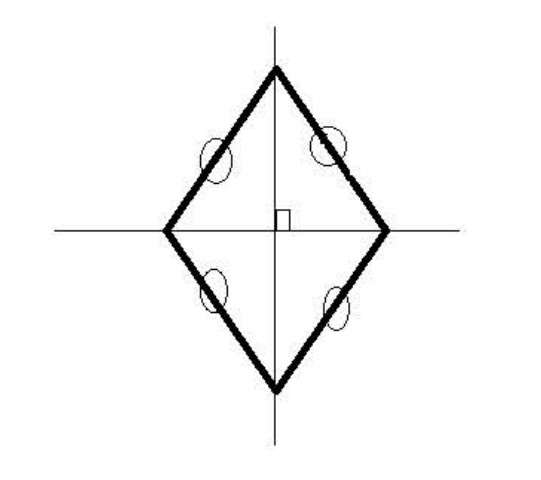
ت) المعين:
تعريف:
المعين هو رباعي أضلاعه الأربعة متقايسة، قطراه متعامدان وكل قطر يمثل محور تناظر للمعين (لاحظ الشكل 01).
تذكير:
قطرا المعين متعامدان وكل منهما محور تناظر له.
الدائرة
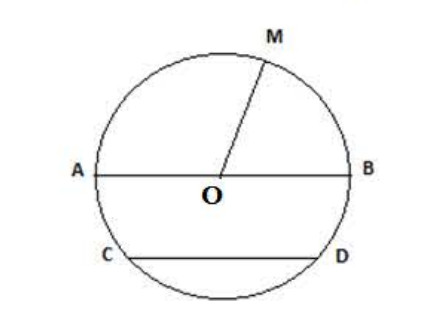
ث) الدائرة:
تعريف:
تتكون الدائرة من كل النقط التي لها نفس البعد عن النقطة الثابتة تسمى المركز.
لدينا الدائرة التالية (لاحظ الشكل 01):
- المسافة بين نقطة من الدائرة والمركز يمثل نصف القطر مثل: .
- يسمى قطر الدائرة.
- يسمى وتر الدائرة.
- يمثل قوس الدائرة.
تذكير:
كل قطر لدائرة هو محور تناظر لها.