ملخص الدرس / الثانية متوسط/رياضيات/الأنشطة الهندسية/التناظر المركزي

1) التناظر المركزي:

عناصر الدرس:

- التعرف على شكل يقبل مركز تناظر.

- نظير نقطة بالنسبة إلى نقطة.

- نظير قطعة مستقيم بالنسبة إلى نقطة.

- نظير نصف مستقيم بالنسبة إلى نقطة.

- نظير زاوية بالنسبة إلى نقطة.

- مركز تناظر شكل.

ا) التعرف على شكل يقبل مركز تناظر:

تعريف:

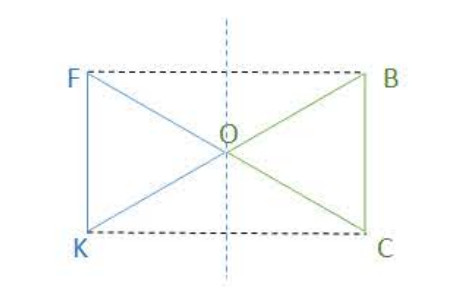
نقول عن شكلين أنهما متناظران بالنسبة إلى نقطة إذا تطابقا بعد التدوير بنصف دورة حول هذه النقطة.

 مثال (لاحظ الشكل 01):

نقول أن المثلث  هو نظير المثلث  بالنسبة إلى 

فيديوا تعليمي للإختبار الأول للفصل الأول:

ب) نظير نقطة بالنسبة إلى نقطة:

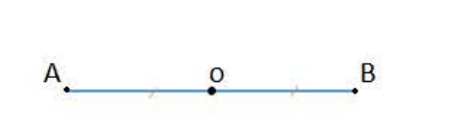
تعريف:

تكون النقطتين  و  متناظرتين بالنسبة إلى النقطة  إذا كانت  منتصف القطعة .

مثال (لاحظ الشكل 01):

نقول أن:

-  هي نظيرة  بالنسبة للنقطة .

-  هي نظيرة  بالنسبة للنقطة .

-  و  متناظرتان بالنسبة للتناظر المركزي الذي مركزه  نظيرة النقطة  بالنسبة إلى النقطة  هي نفسها.

ملاحظة:

 نقطة من المستوي فإن  نظيرة  بالنسبة لـ .

2) نظير قطعة مستقيم بالنسبة إلى نقطة:

تعريف:

نظير قطعة مستقيم بالنسبة إلى  هو قطعة مستقيم تقايسها (لاحظ الشكل 01).

مثال:

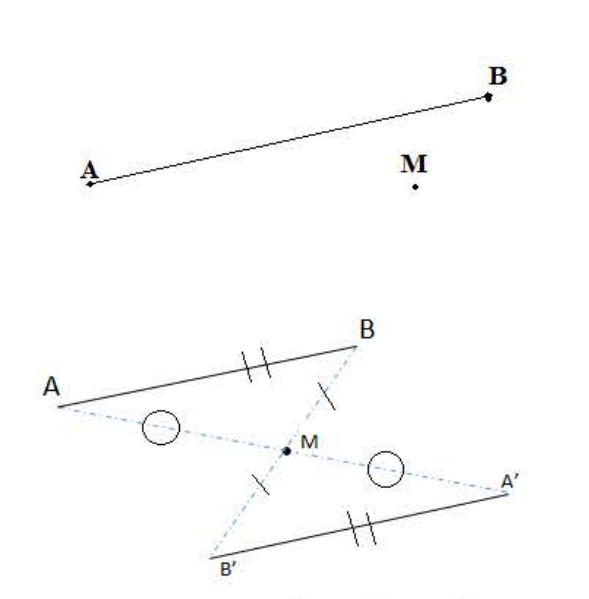
 قطعة مستقيم و  نقطة لا تنتمي إليها كما في الشكل التالي (لاحظ الشكل 02):

أنشى القطعة  نظيرة القطعة  بالنسبة إلى النقطة .

- ننشئ  و  نظيرتي  و  على التوالي بالنسبة للنقطة  حيث: .

نلاحظ أن  و .

أ) نظير نصف مستقيم بالنسبة إلى نقطة:

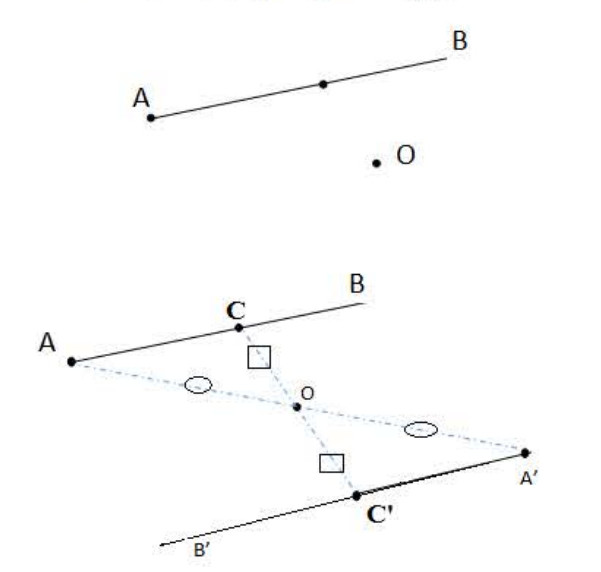
تعريف:

نظير نصف مستقيم  بالنسبة إلى النقطة  هو نصف المستقيم  حاملاهما متوازيان و  نظيرتي  على الترتيب بالنسبة للنقطة  (لاحظ الشكل 01).

مثال:

أنشى نظير لنصف المستقيم  بالنسبة للنقطة .

- الحل:

نظير نصف مستقيم  بالنسبة إلى  هو نصف المستقيم  (لاحظ الشكل 02).

ملاحظة:

نظير نصف مستقيم بالنسبة إلى نقطة هو نصف مستقيم يعاكسه.

ب) نظير زاوية بالنسبة إلى نقطة:

قاعدة:

نظير زاوية بالنسبة إلى نقطة هي زاوية تقايسها ورأسيهما متناظران.

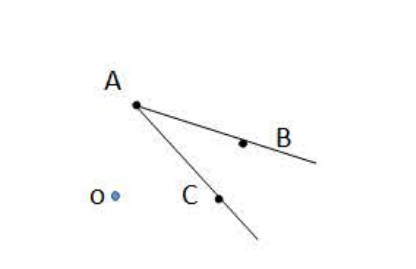
مثال:

لدينا الشكل التالي:

- أنشى الزاوية  نظيرة الزاوية  بالنسبة للنقطة  (لاحظ الشكل 01).

ت) مركز تناظر شكل:

تعريف:

نسمي نقطة  مركز تناظر شكل كيفي إذا كان نظير هذا الشكل بالنسبة إلى النقطة  هو الشكل نفسه.

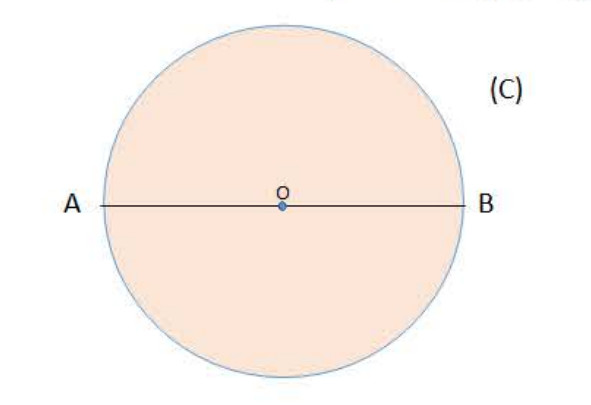
مثال (لاحظ الشكل):

- مركز تناظر الدائرة  هو النقطة .

- مركز تناظر  هو  لأنه منتصفها.

تذكير:

1- التناظر المركزي يحفظ الإستقامية.

2- التناظئر المركزي يحفظ الأطوال.

3- التناظر المركزي يحفظ أقياس الزوايا.

4- التناظر المركزي يحفظ المساحات.