ملخص الدرس / الثانية متوسط/رياضيات/الأنشطة الهندسية/متوازي الأضلاع
الملخص
من الأستاذ(ة) ELBEY Mouloudمتوازي الأضلاع
عناصر الدرس:
- متوازي الأضلاع.
- خواص متوازي الأضلاع.
- خواص متوازي الأضلاع الخاصة.
- مساحة متوازي الأضلاع.
1) متوازي الأضلاع:
تعريف:
متوازي الأضلاع هو شكل رباعي، فيه كل ضلعين متقابلين متوازيان.
مثال:
لدينا:
خواص متوازي الأضلاع
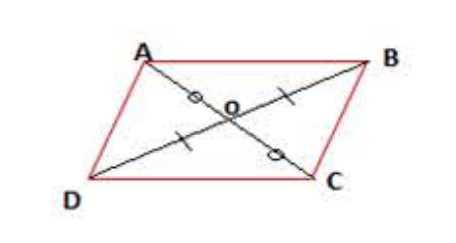
2) خواص متوازي الأضلاع:
خاصية (01):
يتقاطع قطري متوازي الأضلاع في نقطة تمثل منتصف كل منهما.
ملاحظة:
- نقطة تقاطع القطرين هي مركز تناظر متوازي الأضلاع.
- قطري الرباعي متناصفين.
مثال:
متوازي أضلاع إذن:
- هي منتصف
أي:
.
- هي منتصف
أي:
فيديوا تعليمي حول الدرس:
خواص متوازي الأضلاع
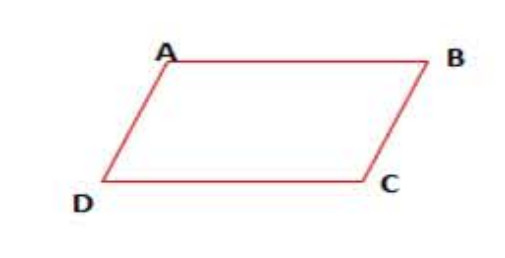
خاصية (02):
في متوازي الأضلاع، كل ضلعين متقابلين، لهمنا نفس الطول ومتوازيان.
مثال:
متوازي أضلاع إذن:
- و
.
- و
.
خواص متوازي الأضلاع
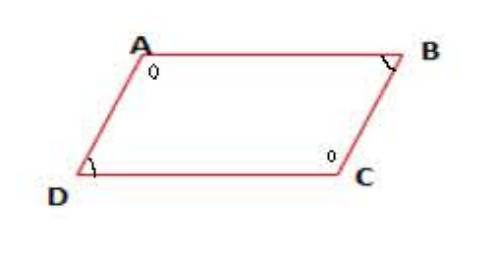
خاصية 03:
في متوازي الأضلاع كل زاويتين متقابلتين لهما نفس القيس.
مثال:
خواص متوازي الأضلاع
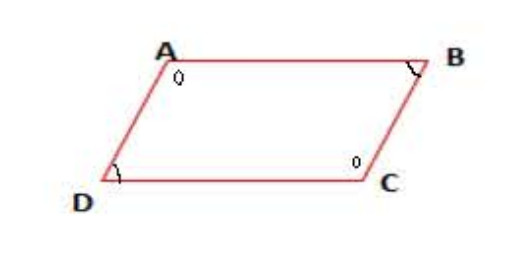
خاصية 04:
في متوازي الأضلاع كل زاويتين متتاليتين متكاملتان (لاحظ الشكل).
مثال:
متوازي أضلاع إذن لدينا:
180°
180°
180°
180°
قاعدة:
لإثبات أن رباعي يكون متوازي أضلاع يكفي أن تتحقق إحدى الشروط التالية:
- كل ضلعين متقابلين متوازيان.
- كل ضلعين متقابلين متقايسان.
- القطران متناصفان.
- كل زاويتين متقابلتين لهما نفس القيس.
- كل زاويتين متتاليتين متكاملتين.
خواص المستطيل
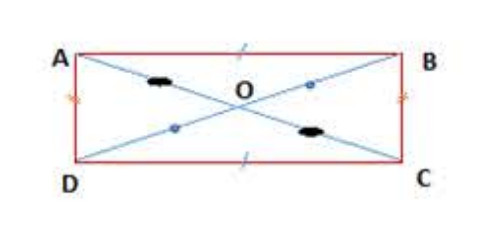
3) خواص متوازيات الأضلاع الخاصة:
أ) أولا: المستطيل
تعريف:
المستطيل هو متوازي أضلاع زواياه قائمه (لاحظ الشكل).
قاعدة:
- زواياه الأربعة قائمة 90° .
- قطرا المستطيل متناصفان ومتقايسان منه:
و
.
- نقطة تقاطع قطراه هي مركز تناظر المستطيل.
- محاور تناظر المستطيل هما محاور أضلاعه.
لإثبات أن رباعي هو مستطيل نتحق من وجود إحدى الخواص السابقة.
خواص المعين
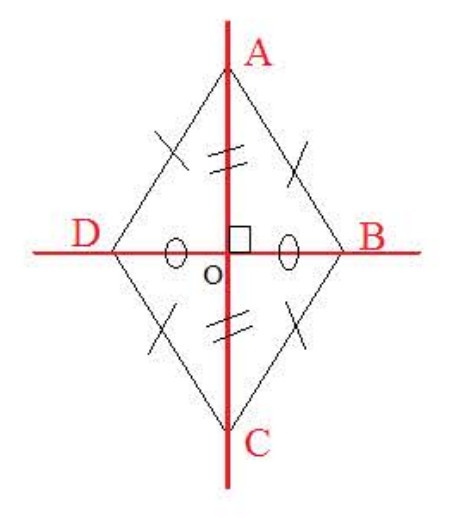
ب) ثانيا: المعين
تعريف:
المعين هو متوازي أضلاع له ضلعان متتاليان متقايسان (لاحظ الشكل).
قاعدة:
- قطرا المعين متعامدان، ومتناصفان ومنه :
و
.
- أطوال أضلاعه متساوية .
- كل زاويتين متقابلتين لهما نفس القيس و
.
- مركز تناظر المعين هي نقطة تقاطع قطريه.
- محورا تناظر المعين هم قطراه.
لإثبات أن رباعي هو معين يكفي توفر إحدى الخواص السابقة في المربع.
ملاحظة: تنطبق جميع خواص متوازي الأضلاع على المعين.
خواص المربع
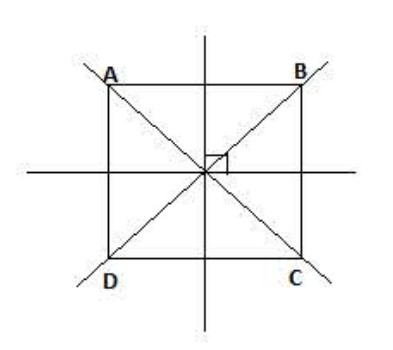
ت) ثالثا: المربع
تعريف:
المربع هو متوازي أضلاع زواياه قائمة وأضلاعه متقايسة.
قاعدة:
- زواياه الأربعة قائمة 90° .
- قطرا المربع متعامدان، متناصفان ومتقايسان
- .
- قطرا المربع ينصفان زواياه.
- مركز تناظر المربع هي نقطة تقاطع قطريه.
- محورا تناظر المربع هما قطراه أو محاور أضلاعه.
لإثبات أن رباعي هو مربع يكفي توفر إحدى الخواص السابقة.
ملاحظة: تنطبق جميع خواص المعين والمستطيل على المربع.
مساحة متوازي الأضلاع
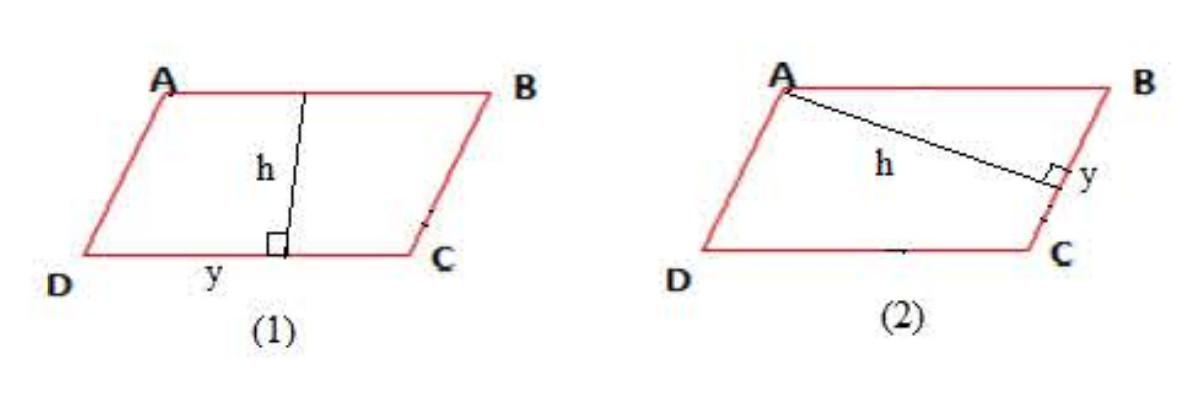
4) مساحة متوازي الأضلاع:
قاعدة:
مساحة متوازي الأضلاع هي جداء طول أحد أضلاعه والإرتفاع المتعلق به: .
ملاحظة:
نعبر عن و
بنفس الوحدة.