ملخص الدرس / الثانية متوسط/رياضيات/الأنشطة الهندسية/الزوايا

الزوايا:

1) الزاويتان المتجاورتان:

تعريف:

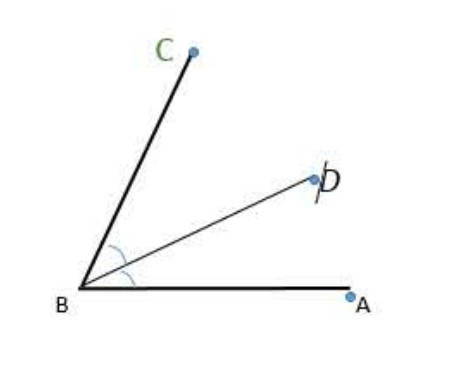
الزاويتان المتجاورتان هما زاويتان لهما نفس الرأس وتشتركان في ضلع يفصل بينهما.

مثال (لاحظ الشكل):

الزاويتان  و  تسميان زاويتان متجاورتان.

فيديوا تعليمي حول الدرس:

2) الزاويتان المتكاملتان والزاويتان المتتامتان:

تعريف الزاويتان المتكاملتان:

الزاويتان المتكاملتان هما الزاويتان اللتان مجموع قيسهما 180°.

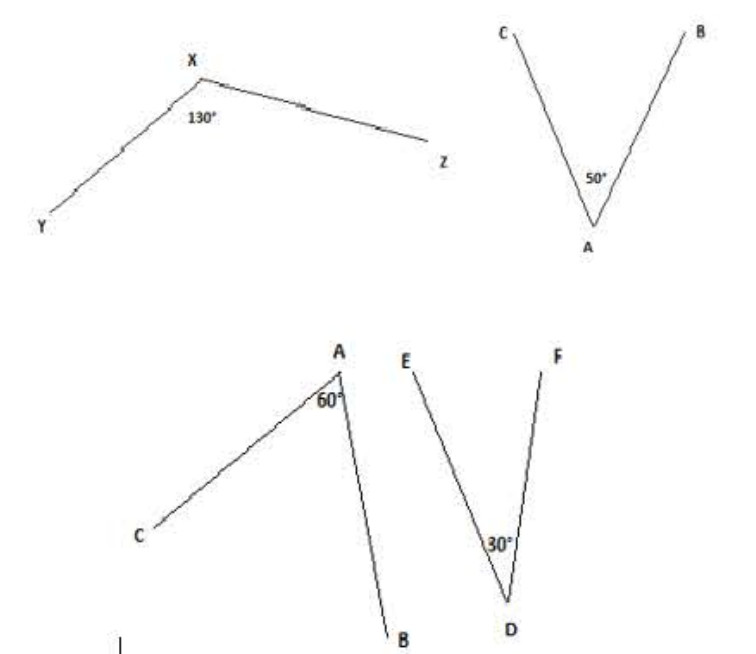
مثال (لاحظ الشكل 01):

الزاويتان  و  متكاملتان لأن:

180° = 130° + 50° 

تعريف الزاويتان المتتامتان:

الزاويتان المتتامتان هما الزاويتان اللتان مجموع قيسهما 90°.

مثال (لاحظ الشكل 02):

الزاويتان  و  ممتامتان لأن:

90° = 30° + 60° 

3) الزاويتان المتقابلتين بالرأس

تعريف:

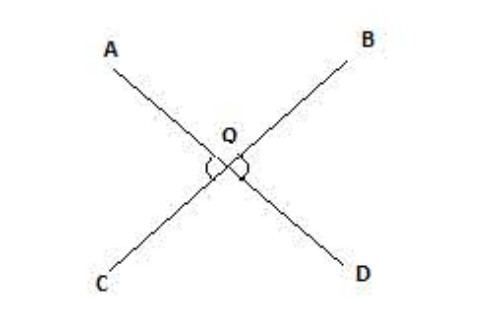
الزاويتان المتقابلان بالرأس لهما رأس مشترك وضلعا إحداهما يعاكسان في الإتجاه ضلعي الأخرى.

مثال (لاحظ الشكل 01):

نلاحظ أن:

متقابلتين بالرأس  و 

متقابلتين بالرأس  و 

خاصية:

كل زاويتان متقابلتين بالرأس لهما نفس القياس.

4) مجموع أقياس زوايا مثلث:

قاعدة:

مجموع قياس زوايا المثلث يساوي 180°.

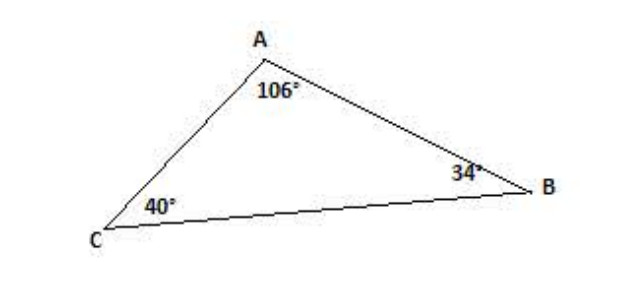
مثال (لاحظ الشكل):

180° = 40° + 34° + 106° 

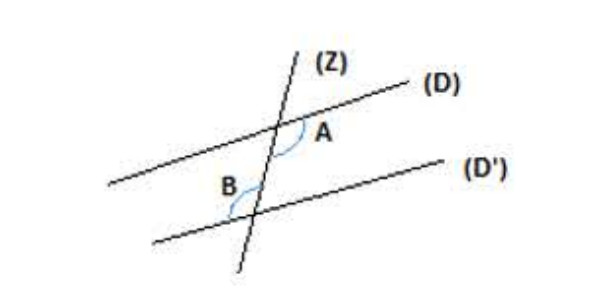
5) الزوايا المعينة بمستقيمين وقاطع لهما:

أ) الزوايتان المتبادلتان داخليا:

قاعدة:

كل زاويتان داخليتان غير متجاورتان وفي جهتين مختلفتين بالنسبة إلى القاطع هما زاويتان متبادلتان داخليا.

مثال (لاحظ الشكل 01):

 و  مستقيمان و  قاطع لهما:

نقول أن الزاويتان  و  متبادلتان داخليا.

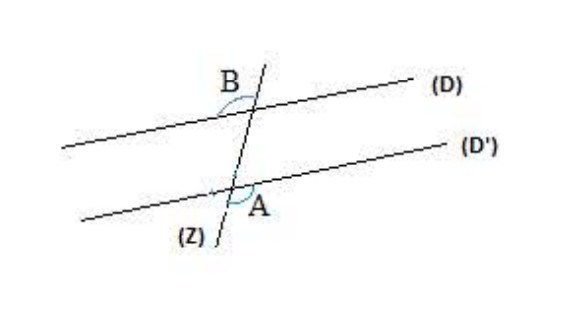
ب) الزاويتان المتبادلتان خارجيا:

كل زاويتان خارجيتان غير متجاورتان وفي جهتين مختلفتين بالنسبة إلى القاطع هما زاويتان مبادلتان خارجيا.

مثال (لاحظ الشكل):

 و  مستقيمان و  قاطع لهما:

نقول أن الزاويتان  و  متبادلتان خارجيا.

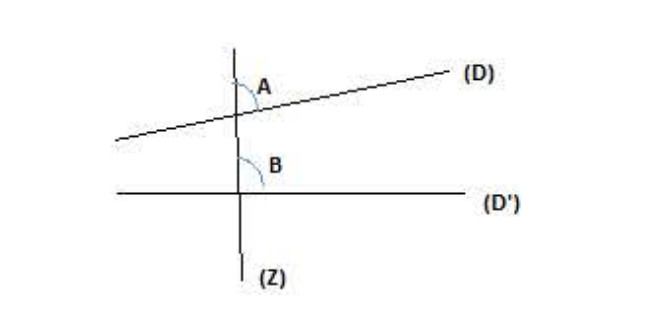
ت) الزاويتان المتماثلتان:

قاعدة:

الزاويتان المتماثلتان هما زاويتان إحداهما داخلية والأخرى خارجية واقعتان في نفس الجهة بالنسبة للقاطع وغير متجاورتان.

مثال (لاحظ الشكل):

 و  مستقيمان و  قاطع لهما:

نقول أن الزاويتان  و  متماثلتان.

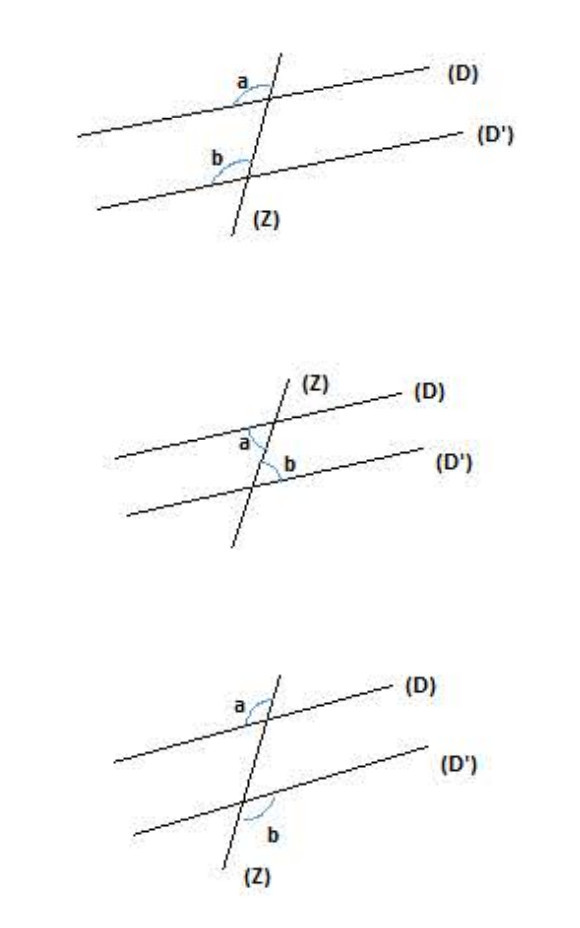
6) خواص الزوايا المعينة بمستقيمين متوازيين وقاطع لهما:

خاصية 01:

إذا قطع مستقيم مستقيمين متوازيين فإن كل زاويتاين متبادلتين داخليا أو خارجيا وكل زاويتين متماثلتين لهما نفس القيس.

مثال 01 (لاحظ الشكل 01):

 و  مستقيمان متوازيان و  قاطع لهما،  و  زاويتان متماثلتان إذن: .

مثال 02 (لاحظ الشكل 02):

 و  مستقيمان متوازيان و  قاطع لهما،  و  زاويتان متبادلتان داخليا إذن: .

مثال 03 (لاحظ الشكل 03):

 و  مستقيمان متوازيان و  قاطع لهما،  و  زاويتان مبتادلتان خارجيا إذن : .

فيديوا تعليمي حول الدرس:

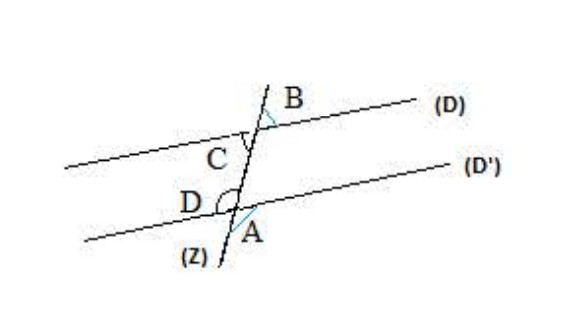
خاصية 02:

إذا قطع مستقيم مستقيمين متوازيان فإن كل زاويتان داخليتين أو خارجيتين واقعتين في نفس الجهة بالنسبة للقاطع متكاملتين.

مثال (لاحظ الشكل 01):

180° 

180° 

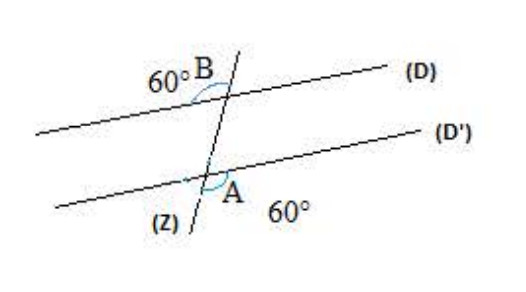
خاصية 03:

العكس: إذا كان مستقيمان يقطعهما قاطع ويحدد زاويتان متبادلتان داخليا أو خارجيا أو زاويتين متماثلتين ولهما نفس القيس إذن المستقيمان متوازيان.

مثال (لاحظ الشكل):

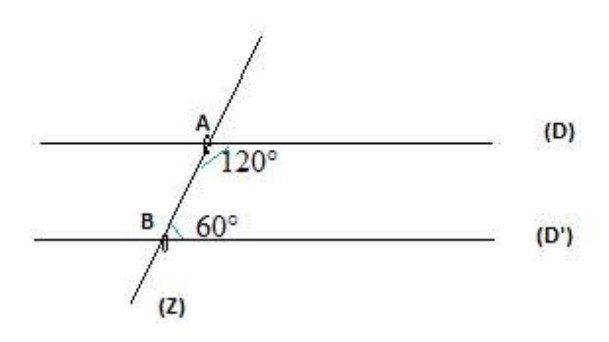
خاصية 04:

يتوازا مستقيمان إذا قطعهما مستقيم وحددا معهما زاويتان داخليتان أو خارجيتان متكاملتان.

مثال (لاحظ الشكل):

 يقطع  و 

180° = 60° + 120° 

إذن: