ملخص الدرس / الثانية متوسط/رياضيات/الدوال و تنظيم المعطيات/تنظيم المعطيات

فهم المعطيات:

عناصر الدرس:

- قراءة وفهم معطيات إحصائية.

- تمثيل معطيات إحصائية.

- تنظيم المعطيات في فئات.

- حساب التكرارات.

1- قراءة وفهم معطيات إحصائية:

تذكير:

لقراءة معطيات إحصائية ممثلة في جدول إحصائي نستعمل طريقة تقاطع الأسطر والعمود لهذا الجدول.

مثال:

الجدول التالي يتضمن نقاط مادة الرياضيات لتلاميذ قسم 2 متوسط المتكون من 30 تلميذ.

- عدد التلاميذ المتحصلين على علامة 10 في الرياضيات هو : 10.

- عدد التلاميذ المتحصلين على علامة 12 في الرياضيات هو: 0.

- عدد التلاميذ المتحصلين على علامة 18 في الرياضيات هو : 5.

2- تمثيل معطيات إحصائية:

يمكننا اختيار مخططات متنوعة لتمثيل معطيات جدول إحصائي من بين هذه المخططات لدينا: مخطط الأعمدة أو المستطيلات والمخطط الدائري.

أ) تعريف مخطط الأعمدة أو المستطيلات:

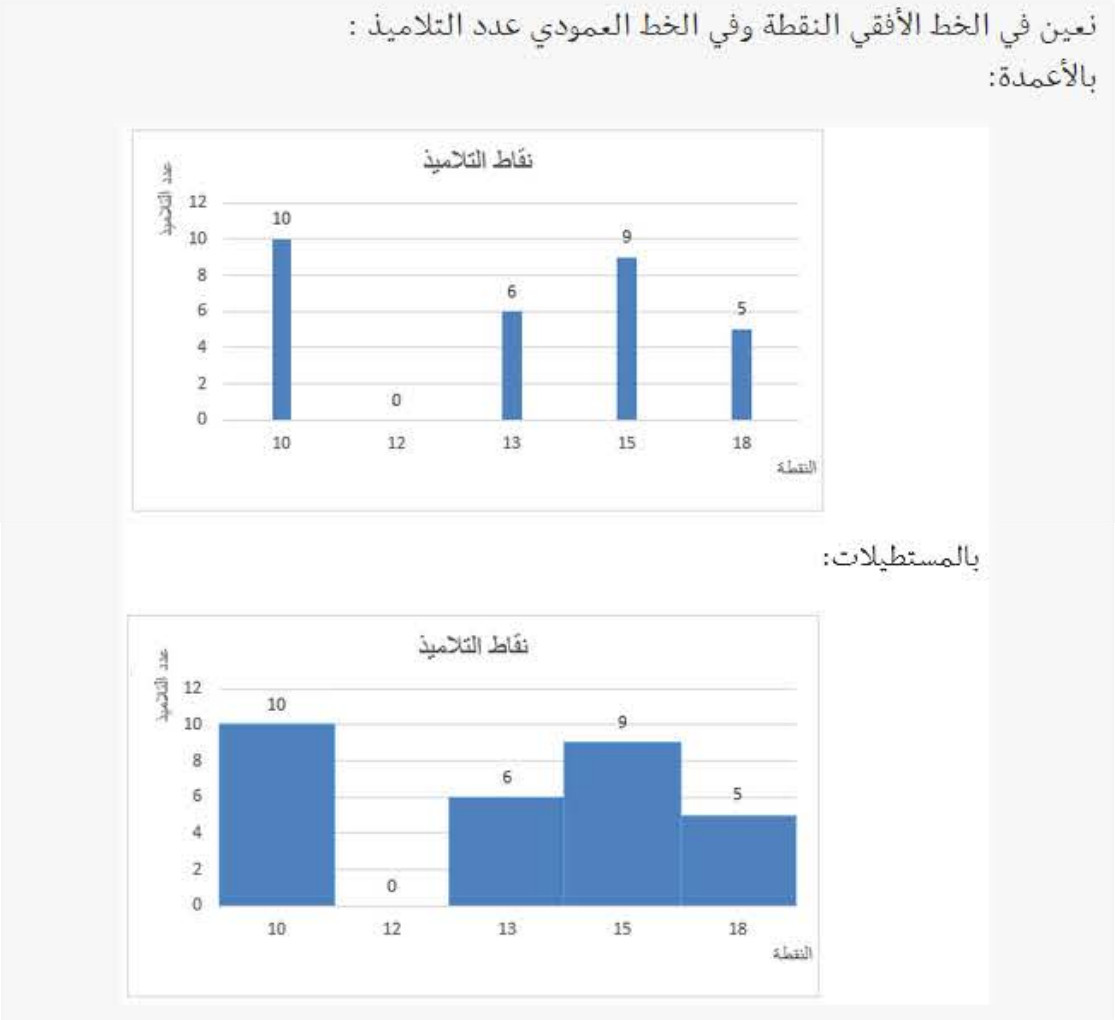
يمكننا أن نمثل المعطيات الإحصائية بالأعمدة أو المستطيلات وذلك من احترام أن تكون ارتفاعات الأعمدة متناسبة مع الأعداد الممثلة لها.

مثال:

نأخذ المثال السابق لرسم المخطط بالأعمدة أو المستطيلات.

الجدول التالي يتضمن نقاط مادة الرياضيات لتلاميذ قسم 2 متوسط المتكون من 30 تلميذ:

 فيديوا تعليمي حول الدرس:

ب) تعريف المخطط الدائري:

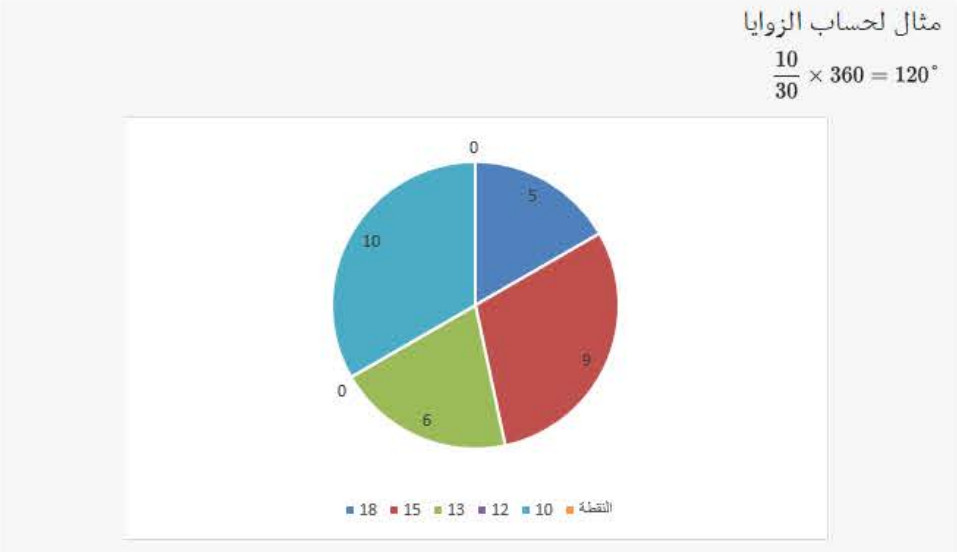
يمكننا أن نمثل معطيات إحصائية بمخطط دائري حيث أن أقياس الزوايا في المخطط الدائري تكون متناسبة مع المقادير الممثلة لها.

مثال:

نكمل مع المثال السابق:

3- تنظيم المعطيات في فئات:

تذكير:

لتقديم بعض المعطيات في فئات وتسهيل قرائتها وتفسيرها، يستحسن أحيانا تجميعها في مجالات تسمى فئات.

فيديوا تعليمي حول الدرس:

مثال:

القائمة التالية تتضمن العلامة التي تحصل عليها التلاميذ في اختبار الرياضيات:

15، 13، 9، 11، 7، 15، 18، 10، 12، 8، 10، 9، 13، 12، 12، 15، 14، 13، 16، 18، 16، 16، 15، 14، 10، 10، 12، 8، 15، 9.

في الجدول التالي تنظم كل العلامات في فئات: نقول أن عدد أفراد الفئة من 7 إلى 10 هو: 10 أي هناك 10 تلاميذ علاماتهم هي: 7، 8، 9، 10.

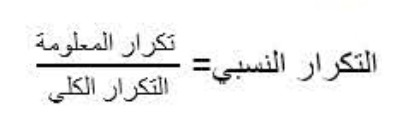
4- حساب التكرارات:

تعريف:

• نسمي تكرار قيمة في معطيات إحصائية عدد مرات ظهور تلك القيمة في المعطيات.
• نسمي تكرار نسبي في معطيات إحصائية حاصل قسمة تكرار هذه القيمة على التكرار الكلي.
• التكرار الكلي هو العدد الكلي للمعطيات.

ملاحظة:

• يمكن كتابة التكرار النسبي لمعلومة على شكل حاصل قسمة أو عدد عشري أو نسبة مئوية.
• 100% مجموع التكرارات النسب المئوية يكون دائما يساوي 1.

مثال:

• يمثل الجدول التالي توزيع مشاركي نادي التنس حسب أعمارهم:
• ما هو تكرار المشاركين الذين عمرهم 16 سنة؟
• ما هو التكرار النسبي للمشاركين الذين أعمارهم 14 سنة؟

نحسب التكرار النسبي في الجدول التالي:

• عدد المشاركين الذين عمرهم 16 سنة هو : 4.
• التكرار الكلي هو عدد كل المشاركين: 30.
• التكرار النسبي للمشاركين الذين أعمارهم 14 سنة هو : 0،23.

ملاحظة:

لإيجاد النسبة المئوية للتكرار النسبي نضرب التكرار النسبي في 100.

مثال:

النسبة المئوية للتكرار النسبي للمشاركين الذين أعمارهم 14 هو  و هو 23,3%