ملخص الدرس / الأولى ثانوي/رياضيات/الجبر و التحليل /العبارات الجبرية

الدرس

من الأستاذ(ة) وزارة التربية الوطنية

العبارات الجبرية

المعاني المختلفة للحرف في عبارة جبرية :

$x$ متغير . مثال : سعر التنقل بسيارة بدلالة المسافة المقطوعة $x \mapsto f\left ( x \right )$ .

$x$ مجهول . مثال : أوجد $x$ في $\mathbb{R}$ حيث $x^{2}=4$ .

$x$ مقدار غير معين . مثال : $E\left ( x \right )$ عبارة معرفة بالشكل $E\left ( x \right )=2x^{2}-3x+5$ .

الاشكال المختلفة لعبارة جبرية :

$C,B,A$ عبارات جبرية :

التسمية	الشكل	مثال	ملاحظات
مجموع	$A+B$	$2x^{2}+3x-1$ مجموع حدوده هي : $-1,3x,2x^{2}$ .	العبارة تتضمن عمليات جمع أو عمليات طرح . يتشكل المجموع من عدة حدود .
جداء	$A\times B$	$x\left ( x-2 \right )$ جداء عاملاه : $\left ( x-2 \right ),x$ .	العبارة لا تتضمن عمليات جمع أو عمليات طرح . يتشكل الجداء من عدة عوامل .
حاصل قسمة	$\frac{A}{B}$	$\frac{x+2}{2x-1}$ حاصل قسمة بسطه $\left ( x+2 \right )$ و مقامه $\left ( 2x-1 \right )$ .	يتشكل حاصل قسمة من بسط مقام .

القيمة العددية لعبارة جبرية :

تعريف :

القيمة العددية لعبارة جبرية هي العدد الذي نتحصل عليه في حالة وجوده عندما نعوض الحروف بأعداد .

ملاحظة :

يمكن ألا تكون اعبارة جبرية قيم عددية ، من أجل بعض قيم الحروف .

قواعد الحساب الجبري

معاني الاقواس :

الاقواس ليس لها نفس الادوار .

طبيعة الأقواس			دور الاقواس
أقواس غير مرتبطة بالحساب .	$\left ( 1 \right )$	أقواس دالة	$A\left ( x \right )$ يعني أن $A$ يتعلق بالمتغير $x$ ، لا يمكن حذف مثل هذه الأقواس .
أقواس مرتبطة بالحساب .	$\left ( 2 \right )$	أقواس متعلقة بجداء	$2x\left ( x-3 \right )$ يعني جداء $\left ( x-3 \right )$ في $2x$ . للتخلص من القوسين ،نوزع $2x$ على حدى المجموع .
	$\left ( 2 \right )$	أقواس متعلقة بجداء	$-2x\left ( 3\times 2x \right )$ يعني جداء $\left ( -2x \right )$ في $3$ في $2x$ .
	$\left ( 3 \right )$	أقواس متعلقة بمجموع	تعني تجميع حدود مجموع .يكون الاستغناء حسب القاعدة الآتية : $D,C,B,A$ عبارات جبرية ، $A+\left ( B+C-D \right )=A+B+C-D$ $A-\left ( B+C-D \right )=A-B-C+D$

المتطابقات الشهيرة :

مبرهنة :

$B,A$ عبارتان جبريتان :

* $\left ( A+B \right )^{2}=A^{2}+2AB+B^{2}$

* $(A-B)^{2}=A^{2}-2AB+B^{2}$

* $\left ( A+B \right )\left (A-B \right )=A^{2}-B^{2}$

تحويل عبارة جبرية

يمكن تحويل عبارة جبرية مكتوبة بصيغة معينة إلى صيغة أخرى باعتماد النشر و التبسيط أو التحليل .

النشر :

نشر جداء يعني كتابته على شكل مجموع .

مثال : $A=\left ( x-1 \right )\left ( -2x+1 \right )-\left ( 2x-1 \right )^{2}$

النشر :

$A=-2x^{2}+x+2x-1-\left ( 4x^{2}-4x+1 \right )$

$A=-2x^{2}+x-2x-1-4x^{2}+4x-1$

تسمى الصيغة الأخيرة للعبارة منشور العبارة $A$ .

تبسيط عبارة :

تبسيط عبارة يعني كتابتها بأقل عدد ممكن من الحدود .

مثال : $A=\left ( x-1 \right )\left ( -2x+1 \right )-\left ( 2x-1 \right )^{2}$

النشر : $A=-2x^{2}+x+2x-1-4x^{2}+4x-1$

التبسيط : $A=\left (-2-4 \right )x^{2}+\left ( 1+2+4 \right )x-1-1$

$A=-6x^{2}+7x-2$

التحليل :

تحليل عبارة يعني كتابتها على شكل جداء .

مثال : $A=\left ( x-1 \right )\left ( -2x+1 \right )-\left ( 2x-1 \right )^{2}$

نكتب : $A=\left ( x-1 \right )\left ( -2x+1 \right )-\left ( 2x-1 \right )^{2}$

$A=\left ( 2x+1 \right )\left [-\left ( x-1 \right )-\left ( 2x-1 \right ) \right ]$

$A=\left ( 2x+1 \right )\left [-x+1- 2x+1 \right ) \right ]$

$A=\left ( 2x+1 \right )\left [-3x+2 \right ) \right ]$

نسمي الصيغة الأخيرة للعبارة الصيغة المحللة للعبارة $A$ .

ملاحظة :

في المتطابقات الشهيرة ، يظهر كل من النشر و التحليل كما في المخطط .

Chargement en cours, Veuillez patientez...

الدوال و العبارات الجبرية

مثال :

الدالة $f:x \mapsto \left (2x-1 \right )^2$

$f$ هي الدالة المعرفة على $\mathbb{R}$ بالشكل $f\left ( x \right ) =\left (2x-1 \right )^2$ .

للحصول على $f\left ( x \right )$ ، نضرب $x$ في $2$ و نطرح $1$ ثم نربع النتيجة .

لدينا $\textrm{u}\left ( x \right )=2x-1$ ، $\textrm{v}\left ( 2x-1 \right )=\left ( 2x-1 \right )^{2}$

منه : $f\left ( x \right )=\textrm{v}\left ( \textrm{u} \left ( x \right )\right )=\left ( 2x-1 \right )^{2}$

Chargement en cours, Veuillez patientez...

ننتقل من $x$ إلى $f\left ( x \right )$ بتطبيق دالتين مرجعيتين على التوالي : الدالة التآلفية $\textrm{u}$ ثم الدالة مربع $\textrm{v}$ .

المساويات و المعادلات

* المساويات :

خواص :

* تكون المساواة صحيحة دائما من أجل كل القيم المعطاة للحروف .

مثال : المتطابقات الشهيرة هي مساويات :

$\left ( 2+3 \right )^{2}=2^{2}+2\times 2\times 3+3^{2}=25$

$\left ( 2-3 \right )^{2}=2^{2}-2\times 2\times 3+3^{2}=1$

$\left ( \sqrt{2}+1 \right )\left ( \sqrt{2}-1 \right )=\left ( \sqrt{2} \right )^{2}-1^{2}=2-1=1$

* نكتب مساواة عند :

- إجراء حساب جبري .

- تعريف دالة أو عبارة .

مثال :

$b,a$ عددان حقيقيان ، $\left ( a+b \right )^{2}-3ab=a^{2}-ab+b^{2}$

من أجل الدالة $f$ التي ترفق بكل عدد حقيقي $x$ مربعه ، نكتب : $x \mapsto f(x)=x^2$

$E$ جبرية بحيث : $E(x)=\frac{x}{x^{2}-1}$

* تسمح المساواة باستعمال مبدأ التعويض في برهان .

مثال :

إذا كان $A=B$ ، فيمكن استبدال العبارة $A$ بالعبارة $B$ .

* المعادلات :

خواص :

* أمام معادلة يطرح تساؤل :

هل يوجد عدد ( أو أعداد ) $x$ من $D$ تحقق المساواة ...؟

نسمي $D$ المجموعة المرجعية للمعادلة .

مثال : هل يوجد عدد حقيقي $x$ حيث $2\left ( x+1 \right )=3x-5$

$x$ هو المجهول .

* حل معادلة ذات المجهول $x$ يعني تعيين كل قيم $x$ من $D$ التي تحققها .

مثال : $7$ حل للمعادلة $2\left ( x+1 \right )=3x-5$ لأنه عند تعويض $x$ بالعدد ، تتحقق المساواة $2\left ( 7+1 \right )=7\times x-5$

*نقول عنةمعادلتين إنهما متكافئتان عندما يكون لهما نفس مجموعة الحلول

إذا أضفنا نفس العدد إلى طرفي معادلة نحصل على معادلة مكافئة لها

إذا ضربنا في نفس العدد غير المعدوم طرفي معادلة نحصل على معادلة مكافئة لها

مثال :

المعادلة $2x-3=8$ تكافئ $2x-3+3=8+3$ أي $2x=11$

و تكافئ $2x\times \frac{1}{2}=11\times \frac{1}{2}$ أي $x=\frac{11}{2}$ .

حل المعادلة $2x-3=8$ هو العدد $x=\frac{11}{2}$ .

* معادلات يؤول حلها إلى حل معادلات من الدرجة الأولى ذات مجهول واحد :

معادلة جداء :

مبرهنة :

يكون جداء عدة عوامل معدوما إذا و فقط إذا كان أحد العوامل على الأقل معدوما .

$A\left ( x \right )\times B\left ( x \right )=0$ تكافئ $A\left ( x \right )=0$ أو $B\left ( x \right )=0$ .

ملاحظة :

مثل المعادلة $A\left ( x \right )\times B\left ( x \right )=0$ تسمى " معادلة جداء " .

نتيجة :

$n$ عدد طبيعي غير معدوم .

$\left [A\left ( x \right ) \right ]^{n}=0$ تكافئ $A\left ( x \right )=0$ .

معادلة حاصل قسمة :

مبرهنة :

المعادلة $\frac{A\left ( x \right )}{B\left ( x \right )}=0$ تكافئ $A\left ( x \right )=0$ أو $B\left ( x \right )\neq 0$ .

ملاحظة :

مثل المعادلة $\frac{A\left ( x \right )}{B\left ( x \right )}=0$ ، تسمى " معادلة حاصل قسمة "

المتراجحات

*إشارة العبارة 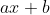$ax+b$ حيث $\left ( a\neq 0 \right )$ :

لدراسة إشارة العبارة $ax+b$ حيث $\left ( a\neq 0 \right )$ ، نحل في $\mathbb{R}$ ، إحدى المتراجحتين $ax+b\geq0$ أو $ax+b\leq0$ و نلخص النتائج كالآتي :

Chargement en cours, Veuillez patientez...

قاعدة :

يمكن تلخيص إشارة العبارة $ax+b$ كما هو موضح في الجدول المقابل :

Chargement en cours, Veuillez patientez...

المتراجحات :

* متراجحة جداء :

مبرهنة :

$A(x)$ ، $B(x)$ عبارتان جبريتان .

المتراجحة $A\left ( x \right )\times B\left ( x \right )\geq 0$ تكافئ $A(x)$ و $B(x)$ من نفس الاشارة .

ملاحظة :

مثل المتراجحة $A\left ( x \right )\times B\left ( x \right )\geq 0$ تسمى " متراجحة جداء " .

* متراجحة " حاصل قسمة " :

مبرهنة :

$A(x)$ ، $B(x)$ عبارتان جبريتان .

المتراجحة $\frac{A\left ( x \right )}{B\left ( x \right )}\geq0$ تكافئ $A\left ( x \right )\times B\left ( x \right )\geq 0$ أو $B\left ( x \right )\neq 0$ .

ملاحظة :

مثل المعادلة $\frac{A\left ( x \right )}{B\left ( x \right )}\geq0$ ، تسمى متراجحة " حاصل قسمة " .

العبارة ax2+bx+cحيث a لاتساوي 0

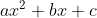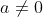العبارة $ax^{2}+bx+c$ حيث $a\neq 0$ :

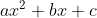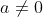* الشكل النموذجي للعبارة $ax^{2}+bx+c$ مع $a\neq 0$ :

تعريف :

العدد $b^{2}-4ac$ هو مميز العبارة $ax^{2}+bx+c$ و نرمز إليه بالرمز $\Delta$ ( نقرأ " دلتا " ).

$a\left [ \left ( x+\frac{b}{2a} \right )^{2}-\frac{\Delta }{4a^{2}} \right ]$ هو الشكل النموذجي للعبارة $ax^{2}+bx+c$ ( $a\neq 0$ ) .

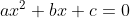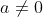* حل المعادلة $ax^{2}+bx+c=0$ ( $a\neq 0$ ) :

لتكن المعادلة $ax^{2}+bx+c=0$ مع $a\neq 0$ ، $\Delta$ مميزها :

- إذا كان $\Delta>0$ فإن المعادلة تقبل حلين $x_{1}$ ، $x_{2}$ : $x_{1}=\frac{-b-\sqrt{\Delta}}{2a}$ ، $x_{2}=\frac{-b+\sqrt{\Delta}}{2a}$

و ينتج $ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$

- إذا كان $\Delta =0$ فأن المعادلة تقبل حلا مضاعفا $x_{0}$ : $x_{0}=\frac{-b}{2a}$ ( نعني بحل مضاعف ، حلين متطابقين ) و ينتج $ax^{2}+bx+c=a(x-x_{0})^{2}$ .

- إذا كان $\Delta < 0$ فإن المعادلة لا تقبل حلولا و العبارة $ax^{2}+bx+c$ لا تحلل .

للمزيد من التفاصيل اليك الفيديوهات التالية :

الفيديو الأول :

ملخص الدرس / الأولى ثانوي/رياضيات/الجبر و التحليل /العبارات الجبرية

الدرس

العبارات الجبرية

المعاني المختلفة للحرف في عبارة جبرية :

الاشكال المختلفة لعبارة جبرية :

القيمة العددية لعبارة جبرية :

تعريف :

ملاحظة :

قواعد الحساب الجبري

معاني الاقواس :

المتطابقات الشهيرة :

مبرهنة :

تحويل عبارة جبرية

النشر :

تبسيط عبارة :

التحليل :

ملاحظة :

الدوال و العبارات الجبرية

المساويات و المعادلات

* المساويات :

خواص :

* المعادلات :

خواص :

* معادلات يؤول حلها إلى حل معادلات من الدرجة الأولى ذات مجهول واحد :

معادلة جداء :

مبرهنة :

ملاحظة :

نتيجة :

معادلة حاصل قسمة :

مبرهنة :

ملاحظة :

المتراجحات

*إشارة العبارة حيث :

قاعدة :

المتراجحات :

* متراجحة جداء :

مبرهنة :

ملاحظة :

* متراجحة " حاصل قسمة " :

مبرهنة :

ملاحظة :

العبارة ax2+bx+cحيث a لاتساوي 0

العبارة حيث :

* الشكل النموذجي للعبارة مع :

تعريف :

* حل المعادلة ( ) :

*إشارة العبارة $ax+b$ حيث $\left ( a\neq 0 \right )$ :

العبارة $ax^{2}+bx+c$ حيث $a\neq 0$ :

* الشكل النموذجي للعبارة $ax^{2}+bx+c$ مع $a\neq 0$ :

* حل المعادلة $ax^{2}+bx+c=0$ ( $a\neq 0$ ) :