ملخص الدرس / الأولى ثانوي/رياضيات/الهندسة/الهندسة المستوية

* تعريف :

متوازي الأضلاع هو رباعي حاملا كل ضلعين متقابلين فيه متوازيان .

مثال :   متوازي الاضلاع معناه :   و  .

* خواص : 

من  أجل كل رباعي  :

       و  متناصفان معناه  متوازي أضلاع .

      و   معناه  متوازي أضلاع .

      و  معناه  متوازي أضلاع .

       و   معناه  متوازي أضلاع .

متوازيات الأضلاع الخاصة : 

* المعين : 

هو متوازي أضلاع له ضلعان متتاليان متقايسان .

مثال : 

       معين معناه  و  متناصفان .

       معين معناه 

     إذا كان  معينا فإن :  ينصف كلا من الزاويتين  و  و  ينصف كلا من الزاويتين  و  .

* المستطيل : 

هو متوازي أضلاع له زاوية قائمة .

مثال : 

    مستطيل  معناه :  

    مستطيل  معناه :  و  متناصفان .

*المربع : 

هو متوازي أضلاع له ضلعام متتاليان متقايسان وزاوية قائمة .

مثال :

  مربع  معناه :  

    مربع  معناه :  و   و   متناصفان .

المثلثات الخاصة :

المثلث متساوي الساقين .

              - فيه ضلعان متقايسان .

              - 

 المثلث متقايس الاضلاع 

            -أضلاعه متقايسة 

            - 

 المثلث قائم الزاوية 

       - فيه زاوية قائمة 

       - 

المستقيمات الخاصة : 

  * الارتفاع : 

في مثلث هو المستقيم الذي يشمل أحد رؤوس المثلث و يعامد الضلع المقابل .

       - ارتفاعات مثلث متقاطعة في نقطة واحدة .

       - نرمز  إلى مساحة المثلث  .

* المحور : 

في مثلث هو محور أحد اضلاعه .

         - محاور مثلث متقاطعة في نقطة واحدة .

         - نقطة تقاطع محاور مثلث هي مركز الدائرة المحيطة بهذا المثلث ( التي تشمل رؤوسه ) .

* المتوسط : 

في مثلث هو المستقيم الذي يشمل أحد رؤوس المثلث و منتصف الضلع المقابل .

               - متوسطات مثلث متقاطعة في نقطة واحدة .

               - نقطة تقاطع متوسطات مثلث هي مركز ثقل هذا المثلث .

* المنصف : 

في مثلث هو منصف إحدى زواياه .

                - المنصفات الداخلية في مثلث متقاطعة في نقطة واحدة .

                - نقطة تقاطع المنصفات الداخلية في مثلث هي مركز الدائرة المرسومة ذاخل هذا المثلث ( أي التي تمس أضلاع المثلث من الداخل ) .

**مبرهنة فيثاغورس و عكسها : 

مبرهنة 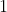 : ( مبرهنة فيثاغورس )

إذا كان  مثلثا قائما في  فإن  .

مبرهنة 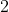 : ( عكس مبرهنة فيثاغورس )

إذا كان في مثلث   ،   فإن المثلث  قائم في  .

نتائج :

إذا كان  مثلثا قائما في   و  الارتفاع المتعلق بالضلع  فإن :

         أ)  

        ب) 

        ج) 

        د)  

** النسب المثلثية في مثلث قائم :

تعريف :

  مثلث قائم في   .

 - جيب الزاوية  : 

 طول الشلع المقابل ل / طول الوتر 

 - جيب تمام  الزاوية  : 

 طول الشلع المجاور ل / طول الوتر

 - ظل الزاوية  : 

طول الشلع المقابل ل /طول الشلع المجاور ل  

خواص : 

       أ )    من التعريف نجد أن : 

      ب ) باستعمال مبرهنة فيثاغورس يمكن أن نبين أن : 

** مبرهنة طالس و عكسها :

مبرهنة طالس :

إذا كان لدينا مستقيمان متقاطعان في نقطة  يقطعهما مستقيمان  و  في النقط  حسب أحد الشكلين أعلاه ، و كان  يوازي  ، فإن  : 

أطوال أضلاع المثلث  متناسبة مع أطوال الأضلاع الموافقة لها من المثلث  أي :   .

عكس مبرهنة طالس : 

إذا كانت كل من النقط  و النقط  على استقامة واحدة و بنفس الترتيب حسب أحد الشكلين أعلاه ، و كان  ، فإن : 

 يوازي 

 هو  و   هو  .

حالة خاصة : مستقيم المنتصفين في مثلث 

 مثلث كيفي  و  نقطتان من  و  على الترتيب :

    - إذا كان النقطتان  و  منتصفي  و  على الترتيب فإن :  و 

    - إذا كانت النقطة  منتصف  و كان  فإن  منتصف  .

مفردات و اصطلاحات : 

 دائرة مركزها  ، و    نقط من الدائرة  حيث  تنتمي إلى   .

*  تسمى قطرا ، و كل من   تسمى وترا في الدائرة  .

 النقطتان المتمايزتان  تعينان على الدائرة   قوسين كل منها نرمز لها بالرمز    .

*  مستقيم يشترك مع الدائرة  في نقطة وحيدة  : يسمى     مماسا للدائرة  عند  . 

* الزاوية  رأسها مركز للدائرة : تسمى زاوية مركزية ، نقول انها تحصر القوس  .

* الزاوية  رأسها نقطة من الدائرة : تسمى زاوية محيطية ، نقول إنها تحصر القوس  .

* الزاوية  : تسمى أيضا زاوية محيطية ، نقول إنها تحصر القوس  .

مبرهنة : 

في كل دائرة ، الزاوية المركزية تساوي ضعف الزاوية المحيطية التي تحصر معها نفس القوس .

نتائج : 

 الزاوية المحيطية في دائرة ، التي تحصر نفس القوس . أو تحصر أقواسا متقايسة تكون متقايسة .

 عندما تكون نقطتان  من دائرة متقابلتين قطريا ، و   نقطة من نفس الدائرة و تختلف عن  و    فإن المثلث   قائم في    .

 تكون رؤوس الرباعي المحدب  من نفس الدائرة إذا تحقق أحد الشرطين : 

                             أ ) 

                             ب)   الزاويتان  و  متكاملتان .

**تقايس مثلثين : 

تعريف : 

نقول عن مثلثين أنهما متقايسين إذا كانا قابلين للتطابق .

نتيجة : 

المثلثان المتقايسان أطوال أضلاعهاما متساوية مثنى مثنى ، و زواياهما متقايسة مثنى مثنى .

** خواص ( حالات تقايس مثلثين ) : 

خاصية : يتقايس مثلثين إذا كانت أطوال أضلاعهما متساوية مثنى مثنى .

خاصية  : يتقايس مثلثان إذا تقايست زاوية و الضلعان اللذان يحصرانها من أحد المثلثين مع زاوية و الضلعين اللذين يحصرانها من المثلث الآخر .

خاصية  يتقايس مثلثان إذا تقايس ضلع و الزاويتان المجاورتان له من أحد المثلثين مع ضلع و الزاويتين المجاورتين له من المثلث الآخر .

نتيجة : 

يتقايس مثلثان إذا كان أحدهما صورة للمثلث الآخر بانسحاب  ، أو تناظر محوري أو تناظر مركزي أو دوران .

**تشابه مثلثين : 

تعريف :

نقول عن مثلثين أنهما متشابهان إذا كانت زاوية أحدهما تقايس زوايا الآخر.

ملاحظات :

 يكفي تساوي زاويتين من أحد المثلثين مع زاويتين من المثلث الآخر للقول إن المثلثين متشابهان ، ذلك لأن مجموع زوايا المثلث يساوي .

 إذا كان أحد المثلثين تصغير ( أو تكبير ) للىخر فإن هذين المثلثين متشابهان .

 المثلثان المتقايسان هما مثلثان متشابهان ، و العكس ليس دائما صحيحا .

مبرهنة :

المثلثان المتشابهان أضلاعهما المتماثلة متناسبة .

** خواص ( حالات تشابه مثلثين ) :

خاصية  : يتشابه مثلثان إذا تقايست زاويتان من أحد المثلثين مع زاويتين من المثلث الآخر .

خاصية   :  يتشابه مثلثان إذا تقايست زاوية من أحد المثلثين مع زاوية من المثلث الآخر ، و كان طولا الضلعين الذين يحصران إحدى هاتين الزاويتين متناسبين مع طولي الضلعين الذين يحصران 

الزاوية الأخرى .

خاصية  : يتشابه مثلثان إذا كان أطوال الأضلاع المتماثلة فيها متناسبة .

** نسبة تشابه مثلثين :

تعريف : 

ليكن  و  مثلثين متشابهين ، نسمي نسبة تشابه هذين المثلثين العدد الموجب غير المعدوم   حيث : 

ملاحظات : 

لتكن  نسبة تشابه مثلثين  و حيث  .

 إن  هي ايضا نسبة تشابه للمثلثين  و  .

 إذا كان  فإن المثلث  هو تصغير للمثلث  ، و نسمي  نسبة ( أو معامل ) التصغير .

 إذا كان  فإن المثلث  هو تكبير للمثلث  ، و نسمي  نسبة ( أو معامل ) التكبير .

إذا كان  فإن المثلث  يقايس المثلث  .

** التحويلات النقطية ، تعاريف :

1) تعريف التناظر المحوري : 

 مستقيم ثابت ، التناظر المحوري بالنسبة إلى المستقيم  هو التحويل الذي يرفق بكل نقطة  من المستوي للنقطة  حيث : 

   * إذا كانت  لا تنتمي إلى المستقيم  فإن  محور قطعة المستقيم  .

   * إذا كانت  لا تنتمي إلى المستقيم  فإن  .

2) تعريف التناظر المركزي : 

 نقطة ثابتة ، التناظر المركزي بالنسبة إلى النقطة هو التحويل الذي يرفق بكل نقطة  من المستوي للنقطة  حيث :  منتصف قطعة المستقيم   .

3) تعريف الانسحاب :

 شعاع ثابت ، الانسحاب الذي شعاعه هو التحويل الذي يرفق بكل نقطة من المستوي للنقطة  حيث :  .

4) الدوران : 

   أ) توجيه المستوي : 

    لتكن  دائرة من الستوي ، يمكن أن نحدد على الدائرة  اتجاهين و اتجاهين فقط أحدهما عكس لتجاه حركة عقارب الساعة و يسمى الاتجاه المباشر ( أو الاتجاه الموجب )،

و الآخر مثل اتجاه حركة عقارب الساعة و يسمى الاتجاه غير المباشر ( أو الاتجاه السالب ) .

تعريف : توجيه المستوي يعني اختيار اتجاه واحد على كل دوائر هذا المستوي .

ملاحظة : لتوجيه مستوي عادة ما نختار الاتجاه المباشر ( عكس اتجاه حركة عقارب الساعة ) .

تعريف الدوران : 

 نقطة ثابتة من مستوس موجه ، و  عدد حقيقي حيث 

الدوران في الاتجاه المباشر ( في الاتجاه غير المباشر ) الذي مركزه النقطة  و زايته  هو التحويل الذي يرفق بكل نقطة  من المستوي النقطة  حيث :

           * إذا كانت  فإن 

           * إذا كانت  فإن  و   

              و الثلاثية  مباشرة ( و الثلاثية  غير مباشرة ) .

** التحويلات النقطية ، خواص :

1) النقط الصامدة :

تعريف :

نقول عن نقطة إنها صامدة بتحويل نقطي ، إذا كانت منطبقة على صورتها بواسطة هذا التحويل .

2) حفظ المسافات ( التقايس ) : 

مبرهنة و تعريف : 

كل من التناظر المحوري ، و التناظر المركزي ، و الانسحاب ، و الدوران يحافظ على المسافات .

يسمى التحويل الذي يحافظ على المسافات تقايسا .

3) حفظ أقياس الزوايا : 

مبرهنة : 

إذا كانت ثلاث نقط   في استقامية فإن صورها   بتقايس تكون في استقامية .

نتيجة : 

صورة مستقيم بتقايس ( تناظر محوري ، تناظر مركزي ، انسحاب ، دوران ) هو مستقيم .

4) حفظ أقياس الزوايا :

مبرهنة : 

صورة زاوية بتقايس هي زاوية تقايسها .

1-معالم المستوي

 و  مستقيمان متقاطعان في النقطه  (الشكل)

 نقطه من  ,  نقطه من 

نضع  ,

لدينا  معلم خطي للمستقيم 

و  معلم خطي للمستقيم 

الشعاعان غير معدومين وغير متوازيين 

تعريف 

الثلاثيه  تسمى معلما للمستوي 

النقطه  تسمى مبدأ المعلم

يسمى كل من الشعاعين  شعاع الوحده

المستقيم  الموجه بالشعاع  يسمى محور الفواصل والمستقيم  الموجه بالشعاع   يسمى محور التراتيب 

إذا كان المستوي مزودا بمعلم   نقول إنه منسوب إلى المعلم  الثنائيه  تسمى أساسا للمستوي

أنواع المعالم الأشكال أدناه تبين أنواع المعالم للمستوي

المعلم         المعلم       المعلم           المعلم متعامد

كيفي                                 متعامد متجانس                      متجانس

2- إحداثيا نقطه 

 معلم للمستوى ,  نقطه من المستوي كما في الشكل 

المستقيم الذي يشمل   ويوازي محور التراتيب , يقطع محور الفواصل في النقطه 

والمستقيم الذي يشمل  ويوازي محور الفواصل , يقطع محور التراتيب في النقطه 

الرباعي  متوازي أضلاع 

إذن 

لدينا  حيث  عدد حقيقي و حيث  عدد حقيقي 

 يسمى فاصله  في المعلم الخطي  و يسمى فاصله  في المعلم الخطي  ينتج انه من أجل كل نقطه  من المستوي المزود بمعلم 

يوجد عددان حقيقيان  وحيدان حيث 

تعريف

الثنائيه  حيث 

تسمى إحداثيتي نقطه  في المعلم 

العدد الحقيقي  يسمى فاصله  و  العدد الحقيقي  يسمى ترتيبه 

إذا كان  إحداثيتي  نكتب 

أمثله 

في المعلم  المقابل

إحداثيا  هما 

إحداثيا  هما 

إحداثيا  هما 

إحداثيا  هما 

إحداثيا  هما 

3- إحداثيتي شعاع 

  معلم للمستوي

كل نقطه  من المستوي ترفق بشعاع وحيد  حيث 

إذا كان  هما إحداثيتي  في المعلم  فإن  أي 

إذن من أجل كل شعاع  توجد ثنائيه وحيده  حيث 

تعريف

الثنائيه  حيث 

تسمى إحداثيي شعاع  في الأساس 

نكتب ونقرأ  إحداثيا هما   في الأساس 

 هو الإحداثي الأول و  هو الإحداثي الثاني للشعاع 

ملاحظه 

إذا كان 

فإن النقطه  و الشعاع  لهما نفس الإحداثيين 

إحداثيا الشعاع  في الأساس هما 

الشعاع  هو الشعاع المعدوم , يرمز له 

أمثله 

في معلم  للمستوي ,  و  نقطتان حيث 

إحداثيا الشعاع  هما 

إحداثيا الشعاع  هما 

تساوي شعاعين 

 معلم للمستوي 

و  شعاعان للمستوي 

خاصيه 

إذا وفقط إذا كان  و 

مجموع شعاعين

معلم للمستوي 

خاصيه إذا كان  و  شعاعيين للمستوي  فإن إحداثيي  الشعاع  هما 

الشعاع  يسمى مجموع شعاعين  و 

مثال  و  شعاعان للمستوي المزود بمعلم

إحداثيا الشعاع  هما 

جداء شعاع بعدد حقيقي 

 معلم للمستوي 

خاصيه 

إذا كان شعاعا المستوي و عددا حقيقيا فإن إحداثيي الشعاع  هما 

الشعاع  يسمى جداء الشعاع  بالعدد الحقيقي 

مثال  شعاع للمستوي المزود بمعلم 

إحداثيي الشعاع  هما 

إحداثيا  الشعاع  هما 

ملاحظه

إذا كان إحداثيا  هما  فإن إحداثيي  هما 

نقول عن الشعاعيين و إنهما متعاكسان أو أن الشعاع  هو معاكس الشعاع 

إذا كان الشعاعان و  متعاكسان أي   فإن 

إحداثيا الشعاع 

 معلم للمستوي 

خاصيه

 إذا كان   نقطتين من المستوي , إحداثياتهما على الترتيب  فإن إحداثيي الشعاع  هما 

فعلا : (علاقه شال)  أي 

إحداثيا  هما  وإحداثيا  هما  ,وكذلك إحداثيا  هما 

حسب الخاصيه  المتعلقه  بمجموع شعاعين , ينتج أن  إحداثيي الشعاع  هما  إي أن إحداثيي الشعاع  هما 

مثال

  معلم للمستوي , نقطتان من المستوي 

إحداثيا الشعاع  هما

إحداثيا الشعاع  هما 

4- توازي شعاعين 

المستوي المنسوب إلى معلم 

شعاعان للمستوي

خاصيه

الشعاعان  و  متوازيان إذا وفقط إذا كان 

نفرض أن الشعاعين و  متوازيان ولنبرهن أن

  لدينا و متوازيان  إذن يوجد عدد حقيقي  حيث 

نعلم أن إحداثيي الشعاع  هما 

ومن المساواه ينتج أن  و 

إذن  و  أي أن  إذن 

نفرض أن 

ولنبرهن أن الشعاعان  و متوازيان 

إذا كان  فإن  و  متوازيان 

إذا كان   فإن أحد إحداثييه  أو  , على الأقل , غير معدوم , وليكن مثلا  

المساواه   تكتب

إذن يمكن أن نكتب 

ينتج أن  أي أن الشعاعين  و  متوازيان 

وبالمثل , إذا فرضنا  أن فنحصل على المساواه

ونستنتج كذلك أن و متوازيان

مثال

 ثلاث أشعه  للمستوي المنسوب  إلى معلم 

الشعاعان و  متوازيان لأن 

الشعاعان  و  غير متوازيان لأن 

شعاع توجيه لمستقيم 

 و  نقطتان  مختلفان من المستوي ,هاتان النقطتان تعينان مستقيما يرمز له   أو  أو ...

تعريف

من أجل كل نقطه  من  , يكون منحى الشعاع  هو نفس منحى الشعاع  , الشعاع  هو شعاع توجيه للمستقيم 

كل شعاع غير معدوم  له نفس منحنى  هو شعاع توجيه للمستقيم  في الشكل , كل من الشعاعين  هو شعاع توجيه  للمستقيم 

ملاحظه 

شعاع توجيه مستقيم يعين منحنى هذا المستقيم 

انتبه

لمستقيم  وشعاع  نفس المنحى , يعنى أن  هو شعاع توجيه للمستقيم 

لشعاعين نفس المنحى يعني أنهما متوازيان 

معادلات مستقيم معين بنقطه وشعاع توجيه 

المستوي المنسوب إلى معلم  . مستقيم يشمل  النقطه 

 شعاع توجيه للمستقيم 

إذا كانت  نقطه من المستوي فإن إحداثيتي   هما 

 نقطه من  يعني  , لشعاعين  و  نفس المنحى 

وحسب شرط التوازي شعاعين نكتب 

إذن 

تعريف 

 وعددان حقيقيان غير معدومان في آن واحد 

المعادله  هي معادله مستقيم  المعين بالنقطه ذات الإحداثيين وشعاع توجيه ذي الإحداثيين 

عندما , العدد الحقيقي   يسمى معامل توجيه المستقيم 

ملاحظه 

يمكن كتابه المعادله السابقه في شكل أبسط كما يلي 

1) إذا كان المستقيم  يوازي محور الفواصل فإن ترتيب كل نقطه  من  هو  ترتيب النقطه 

إذن  هي معادله للمستقيم 

2) إذا كان المستقيم  يوازي محور التراتيب فإن  فاصله كل نقطه  من   هو  فاصله النقطه 

إذن  هي معادله مستقيم 

3) إذا كان  لا يوازي كل من المحورين  الإحداثيين , في هذه الحاله  يكون  غير معدومين معا , إذا يمكن كتابه المعادله 

على الشكل المبسط 

مثال :

المعادله  هي معادله مبسطه 

للمستقيم  الذي يشمل النقطه  ويوازي  الشعاع   يمكن أيضا أن نكتب المعادله السابقه على الشكل 

ملاحظه

باستعمال المعادله  نجد

وهو شكل آخر للمعادله السايقه 

معادله مستقيم معين بنقطتين مختلفتين 

المستوي المنسوب إلى معلم  .  المستقيم الذي يشمل  النقطتين المختلفتين  الشعاع ذو الاحداثيين  هو شعاع توجيه المستقيم . إذن  معين بالنقطه  وشعاع توجيه له هو 

بالرجوع إلى معادله مستقيم معرف بنقطه وشعاع توجيه نكتب معادله للمستقيم  وهي

وبعد الإختصار نجد

تعريف

المعادله  هي معادله للمستقيم المعين بنقطتين مختلففتين اللتين إحداثياتهما 

عندما  , العدد  هو معامل توجيه  المستقيم 

ملاحظه 

يمكن كتابه معادله للمستقيم المعرف بالنقطتين على الشكل المبسط كما يلي 

1) إذا كان  يوازي محور الفواصل فإن  لكل نقط  نفس الترتيب 

إذن  هي معادله مستقيم 

2) إذا كان  يوازي محور التراتيب فإن لكل نقط  نفس الفاصله 

إذن   معادله للمستقيم 

3) إذا كان  لا يوازي كل من المحورين الإحداثيين فإن  و  إذن يمكن كتابه معادله  على الشكل 

4) إذاكان  نقطتين مختلفتين من المستوي  حيث  و   فإن  معادله   هي 

مثال 

معادله المستقيم المعين بالنقطتين   يمكن تعيينها  كما يلي 

 نلاحظ أن فاصلتي و مختلفتان ,  وكذلك ترتيبهما 

إذن المستقيم  لا يوازي المحورين  , وباستعمال المعادله السابقه نجد 

بعد التبسيط نحصل على المعادله 

الشكل العام لمعادله مستقيم

معادله مستقيم  معرفه بنقطه  وشعاع توجيه  هي  هي 

إذا وضعنا   فإن المعادله  السابقه تكتب على الشكل  حيث  عددان حقيقيان غير معدومين في آن واحد 

العكس 

يمكن البرهان أن مجموعه النقط  من المستوي التي تحقق  حيث  عددان حقيقيان غير معدومين في آن واحد , هي مستقيم حيث  شعاع توجيه له

نظريه 

عندما  , العدد الحقيقي  هو معامل توجيه  ( أو ميل  إذا كان المعلم متعامدا ومتجانسا )

مثال المستوي المنسوب إلى معلم 

المعادله  هي معادله للمستقيم الذي يشمل النقطه  وشعاع توجيهه 

ملاحظه 

يمكن كتابه  المعادله   كما يلي

إذاكان   فإن   في هذه الحاله نكتب  حيث 

وهي معادله مستقيم  الموازي لمحور التراتيب , شعاع توجيه  هو كل شعاع يوازي 

2) إذا كان  نكتب المعادله  على الشكل 

بوضع   نكتب 

مبرهنه 

كل مستقيم للمستوي له معادله من الشكل 

 إذا كان المستقيم يوازي محور التراتيب 

و  إذا كان المستقيم لا يوازي محور التراتيب

 هو معامل توجيه  المستقيم الذي معادلته  و هو شعاع توجيه له 

3- توازي مستقيمين متوازيان

إذا وفقط إذا كان الشعاعان و متوازيان 

الشعاعان  و متوازيان إذا وفقط إذا كان  و

مبرهنه 

 و مستقيمان للمستوي معادلتهما  و  على الترتيب 

المستقيمان  و متوازيان  إذا وفقط إذا كان 

ملاحظه 

 مستقيم معادلته  و مستقيم معادلته  كل من  المعادلتين تكتب  و 

حيث  

الشعاعان و هما شعاعا توجيه للمستقيم و على الترتيب 

 ومتوازيان  إذا وفقط إذا كان و متوازيان 

مبرهنه

و مستقيمان للمستوي معادلتهما   و على الترتيب 

 و متوازيان إذا وفقطإذا كان 

أي ان و متوازيان  إذا وفقط إذا كان لهما نفس معامل التوجيه 

ملاحظه 

إذا كان المستقيمان  و غير متوازيان فهما متقاطعان