ملخص الدرس / الأولى ثانوي/رياضيات/الهندسة/الهندسة في الفضاء

المنظور متساوي القياس هو تقنية لتمثيل أشياء من الفشاء على سطوح مستوية ( ورقة الكراس ، سبورة ، ....) ، و من قواعد هذه التقنية :

 الخطوط المخفية ( التي لا ترى عند تصور رؤية المجسم ) نرسمها بخطوط متقطعة .

 على مستوى الواجهة ( مستوى الاسقاط ) نحافظ على كل الخواص ( التوازي ، التعامد ، التنصيف ، استقامية النقط ، ....) ، و المقادير ( الزوايا ، المسافات ،....) .

 على جميع الأوجه نحافظ على : استقامية النقط ، و التوازي ، و منتصف قطعة مستقيم ، و كذا للنسب بين قطع المستقيم المتوازية .

مثال :

تمثيل موشور قائم قاعدته مثلث متقايس الاضلاع مرسوم عليه منصف إحدى زوايا القاعدة ، مرة بأخذ القاعدة في مستوى الواجهة ، و مرة أخرى بأخذ أحد الأسطح الجانبية في مستوى الواجهة .    

ملاحظة :

المستوي  في المنظور متساوي القياس يمثل بمتوازي أضلاع .

بديهية  :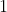

إذا كانت نقطتان  و  متمايزتين فإنه يوجد مستقيم وحيد يشملهما .

     * النقطتان   و  تعينان مستقيما وحيدا ، نرمز له ب  أو  .

 بديهية  :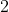

إذا لم تكن ثلاث نقط   و  و  في استقامية فإنه يوجد مستو وحيد يشملها .

    * النقط   و  و  تعين مستو وحيد ، نرمز له ب  أو ب  .

    * نمثل االمستوي في المنظور متساوي القياس بمتوازي أضلاع .

بديهية  :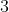

إذا شمل مستو نقطتين متمايزتين   و  فإنه  يشمل كل نقط المستقيم  .

نتيجة : 

يتعين المستوي : 

      إما بثلاث نقط ليست على استقامة واحدة .

      و إما بمستقيم و نقطة لا تنتمي إلى هذا المستقيم .

      و إما بمستقيمين متمايزين متقاطعين أو متوازيين .

    * كل من : 

       - النقط  و  و  

      - المستقيم  و النقطة 

     - المستقيمان المتوازيان  و

     - المستقيمان المتقاطعان  و 

                  تعين نفس المستوي  .

ملاحظة : 

كل خواص و نتائج الهندسة للمستوية تبقى صحيحة في أي مستو من الفشاء .

الأوضاع النسبية لمستويين :

كل مستويين من الفضاء هما : إما متاطعان و إما متوازيان .

الأوضاع النسبية لمستقيم و مستو :

كل مستقيم و مستو من الفضاء هما : إما متقاطعان و إما متوازيان .

الاوضاع النسبية لمستقيمين : 

كل مستقيمين من الفضاء هما : 

              - إما متقاطعان ( فهما من مستو واحد ).

              - إما متوازيان ( فهما من مستو واحد ).

              - و إما ليسا من مستو واحد .

المستقيمات المتوازية في الفضاء : 

 * تعريف : 

 المستقيمان المتوازيان في الفضاء هما مستقيمان متطابقان ، أو من نفس المستوي و غير متقاطعين .

 مثال : الشكل يمثل موشور قائم قاعدته مثلث ، نلاحظ فيه أن : المستقيمين  و متوازيان ، و المستقيمين  و  متقاطعان ، بينما المستقيمان   و 

ليسا من مستو واحد .

 * خواص : 

 يوجد مستقيم وحيد يشمل نقطة معلومة و يوازي مستقيما معلوما .

 إذا قطع مستو أحد مستقيمين متوازيين فإنه يقطع الآخر .

 المستقيمان الموازيان لثالث متوازيان .

المستويات المتوازية : 

 * تعريف : 

 المستويان المتوازيين هما مستويان متطابقان ، أو منفصلان ( لا توجد بينهما أية نقطة مشتركة ) .

  مثال : الشكل يمثل متوازي مستطيلات ، نلاحظ أن المستويين  و  متوازيان ، و المستويين   و متوازيان ،

و كذلك  و  .

* خواص :

 يوجد مستو وحيد يشمل نقطة معلومة و يوازي مستويا معلوما.

 إذا قطع مستقيم أحد مستويين متوازيين فإنه يقطع الآخر .

 إذا قطع مستو أحد مستويين متوازيين فإنه يقطع الآخر ، و يكون مستقيما التقاطع متوازيان .

 المستويان الموازيان لثالث متوازيان .

المستقيمات و المستويات المتوازية :

* تعريف : 

يكون مستقيم و مستو متوازيين إذا كانا منفصلين ( لا توجد بينهما أية نقطة مشتركة ) أو كان المستوي يحتوي المستقيم .

مثال : الشكل يمثل مكعب  نلاحظ فيه أن : المستقيم  يوازي كلا من المستويين  و  ، و كذلك المستقيم  

و يوازي كلا من المستويات  و  و  و  .

* خواص :

 يكون مستقيم موازيا لمستو إذا و فقط إذا كان موازيا لمستقيم من هذا المستوي .

 إذا كان مستقيم يوازي أحد مستويين متوازيين فإنه يوازي المستوي الآخر .

 إذا كان مستقيم يوازي مستويين متقاطعين فإنه يوازي مستقيم تقاطعهما .

  يتوازى مستويان إذا و فقط إذا احتوى احدهما على مستقيمين متقاطعين كل منهما يوازي المستوي الآخر .

تعامد المستقيمات في الفضاء : 

* تعريف :

نقول عن مستقيمين أنهما متعامدان إذا كان المستقيمان الموازيان لهما من نفس النقطة متعامدين .

مثال : الشكل يمثل مكعب نلاحظ فيه ان المستقيمين  و  متعامدان ، لأن  و متعامدان في النقطة  و  و  متوازيان .

* خواص :

 المستقيم العمودي على أحد مستقيمين متوازيين عمودي على الآخر .

 المستقيمان الموازيان لمستقيمين متعامدين متعامدان .

تعامد المستقيمات و المستويات :

*تعريف : 

نقول عن مستقيم أنه عمودي على مستو إذا كان هذا المستقيم عموديا على كل مستقيمات هذا المستوي .

مثال : الشكل يمثل مكعب نلاحظ فيه ان المستقيم    عمودي على كل من المستقيمين   و فهو عمودي على مستويهما  .

* مبرهنة: 

إذا كان مستقيم عموديا على مستقيمين متقاطعين من مستو فإنه عمودي على كل مستقيمات هذا المستوي .

*خواص :

 يوجد مستقيم وحيد يشمل نقطة معلومة و يعامد مستويا معلوما .

 يوجد مستو وحيد يشمل نقطو معلومة و يعامد مستقيما معلوما .

 المستويان الععموديان على نفس المستقيم متوازيان .

 المستقيمان العموديان على نفس المستوي متوازيان .

 المستقيم العمودي على أحد مستويين متوازيين عمودي على الآخر .

 المستوي العمودي على أحد مستقيمين متوازيين عمودي على الآخر .

تعامد المستويات :

* تعريف : 

نقول عن مستويين أنهما متعامدان إذا شمل أحدهما مستقيما عموديا على الآخر .

  مثال : الشكل يمثل متوازي مستطيلات على سبيل المثال  نلاحظ  فيه أن كلا من المستويات  و  و و   

عمودي على المستوي  .

*خواص :

 المستوي العمودي على أحد مستويين متوازيين عمودي عاى الآخر .

 إذا كان  و  مستويين متقاطعين و كان كل منهما عموديا على مستو ثالث  فإن مستقيم تقاطع المستويين  و عمودي على المستوي  .

المستوي المحوري لقطعة مستقيم : 

* تعريف : 

 ،  نقطتان متمايزتان ، نسمي مستويا محوريا لقطعة  المستوي العمودي على  الذي يشمل منتصف   .

* ملاحظتان :

 إذا كان  مستويا محوريا لقطعة المستقيم  ، فكل مستقيم من المستوي  يشمب منتصف  هو محور القطعة  .

 إذا كان  مستويا محوريا لقطعة المستقيم  ، فكل محور للقطعة محتو في المستوي  .

* مبرهنة : 

مجموعة نقط الفضاء المتساوية المسافة عن نقطتين متمايزتين  ،   هي المستوي المحوري لقطعة المستقيم  .

تذكير حول الحجوم :