ملخص الدرس / الأولى ثانوي/رياضيات/الإحصاء/الإحصاء

تمهيد : 

عندما نهتم بدراسة ظاهرة ما ، مثلا عدد الاخوة و الأخوات لتلاميذ المستوى النهائي في ثانوية ما ، نقول أننا نجري دراسة احصائية على مجتمع احصائي هو تلاميذ المستوى النهائي لهذه الثانوية 

و يكون عدد الاخوة و الاخوات في هذه الحالة هو الميزة الاحصائية التي تسمى أيضا الطبع الاحصائي .

نسمي عينة كل جزء من المجتمع الاحصائي ، مثلا كل قسم نهائي في هذه الثانوية هو عينة .

عندما نأخذ الميزة الاحصائية قيما عددية ، نسميها ميزة كمية أو متغيرا احصائيا .

نقول عن المتغير الاحصائي إنه متقطع عندما يمكن عد و حصر قيمه ( عدد الاخوة ) و إنه مستمر عندما يمكن قياس قيمه ( قامات التلاميذ ) .

أحيانا عندما يكون عدد القيم كبيرا ، نلجأ إلى حصرها ضمن مجالات  تدعى فئات و نسمي مركز الفئة العدد  و طولها العدد الموجب  .

نهتم في بعض الاحيان بدراسة ظاهرة نوعية ، كلون العينين أو لون الشعر ، لا يمكن التعبير عليها بعدد فنقول في هذه الحالة أن الطبع الاحصائي هو طبع إحصائي نوعي .

التوزيعات التكرارية : 

* تكرار قيمة الطبع الاحصائي هو عدد الأفراد الموافقة لهذه القيمة .

* تواتر قيمة الطبع الاحصائي هو حاصل قسمة تكرارها على عدد أفراد المجتمع ( أي التكرار الكلي ) .

* نسمي سلسلة احصائية مجموعة القيم  التي جمعت .

* غالبا ما نمثل سلسلة احصائية بجدول يشمل كل قيمة و تكرارها . 

التوزيعات التكرارية المجمعة :

نفرض أن قيم الميزة مرتبة ترتيبا تصاعديا .

* التكرار المجمع الصاعد لقيمة ( أو لفئة ) هو مجموع تكرار هذه القيمة ( أو الفئة ) و تكرارات القيم (أو الفئات ) الأصغر منها .

* التكرار المجمع النازل لقيمة ( أو لفئة )هو مجموع تكرار هذه القيمة ( أو الفئة ) و تكرارات القيم (أو الفئات ) الأكبر منها .

* التواتر المجمع الصاعد لقيمة ( أو لفئة ) هو مجموع تواتر هذه القيمة ( أو الفئة ) و تواترات القيم (أو الفئات ) الأصغر منها .

* التواتر المجمع النازل لقيمة ( أو لفئة ) هو مجموع تواتر هذه القيمة ( أو الفئة ) و تواترات القيم (أو الفئات ) الأكبر منها .

المنوال - الفئة المنوالية :

*تعريف :

* نسمي منوالا لسلسلة ذات متغير إحصائي متقطع ، كل قيمة موافقة لأكبر تكرار و نرمز له  .

* نسمي فئة منوالية لسلسلة ذات متغير إحصائي مستمر ، كل فئة موافقة لأكبر تكرار .

الوسيط :

*تعريف :

اتكن سلسلة إحصائية ذات متغير متقطع قيمه مرتبة ترتيبا تصاعديا أو تنازليا ، و تكرارها الكلي  .

نسمي الوسيط لهذه السلسلة العدد الذي نرمز له بالرمز  ، و المعرف كالآتي :

* إذا كان  فرديا أي  يكون القيمة التي رتبتها  .

* إذا كان زوجيا  أي  يكون نصف مجموع  القيمتين  التين رتبتاهما  و  .

 *خاصية : 

الوسيط يجزئ سلسلة إحصائية مرتبة ترتيبا تصاعديا أو ترتيبا تنازليا إلى جزئين لهما نفس التكرار .

*ملاحظة : 

الوسيط لا يتأثر بالقيم الشاذة ، مثلا : للسلسلتين    و    نفس الوسيط  . 

الوسط الحسابي :

*تعريف : 

الوسط الحسابي للقيم  التي تكراراتها على الترتيب 

هو العدد  حيث  .

*ملاحظة : 

الوسط الحسابي يتأثر بالقيم الشاذة ، مثلا الوسط الحسابي للسلسلة  هو  

الوسط الحسابي للسلسلة  هو  .

*حول الرمز  :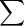

* المجموع  يكتب  و نقرأ :   مجموع الأعداد  من  إلى  .

* يمكن كتابة الوسط الحسابي  على الشكل  .

* خواص الوسط الحسابي : 

     - خاصية  :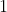

لتكن سلسلة إحصائية نأخذ القيم  بالتواترات  على الترتيب .

الوسط الحسابي لهذه السسلسلة هو العدد  حيث  .

     -خاصية  :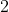

 * عندما نضيف نفس العدد  لكل قيمة من قيم الطبع الاحصائي : يزداد الوسط الحسابي بالمقدار  أي  .

* عندما نضرب نفس العدد  لكل قيمة من قيم الطبع الاحصائي : الوسط الحسابي يضرب في العدد   أي   .

المدى : 

* تعريف : 

 مدى سلسلة إحصائية هو الفرق بين أكبر قيمة للمتغير الاحصائي و أصغر قيمة له .

* ملاحظة :

يسمى كل من المنوال و الوسيط الحسابي مؤشرات الموقع ، بينما يسمى المدى مؤشر التشتت .

رغم ما توفره الجداول الاحصائية من معلومات عن الظاهرة محل للدراسة إلا أنها لا تزودنا بسرعة بفكرة واضحة و مختصرة و شاملة عن هذه الظاهرة . لذلك نلجأ غالبا إلى تمثيل هذه الجداول تمثيلا بيانيا .

التمثيلات البيانية التي نستعملها عادة هي : المخطط بالاعمدة ، المدرج التكراري ، المخطط الدائري ، مضلع التكرارات ، مضلع التواترات .

مثال  :

يعبر الجدول الآتي عن توزيع أعمار  طفلا :

المخطط بالأعمدة المتعلق بهذه السلسلة الاحصائية : 

مثال  :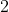

أعمار  طفل موزعة كالأتي :

المدرج التكراري المتعلق بهذه السلسلة الاحصائية هو :

ملاحظة هامة :

مساحات المستطيلات ( الملونة بالاحمر في الشكل ) متناسبة مع التكرارات .

عينة احصائية :

لتكن سلسلة احصائية تتكون من نتائج تجربة اجريت  مرة . هذه السلسلة تشكل عينة .

مثال :

   -التجربة : رمي قطعة نقدية غير مزيفة .

   - النتائج الممكنة : ظهر أو وجه .

   - الترميز : نرمز بالرقم  للوجه و بالرقم  للظهر .

   - العينة  : عندما نرمي هذه القطعة مرات نتحصل على عينة مقاسها  .

            نتحصل مثلا على العينة :  .

سجلنا تواتر كل نتيجة من النتيجتين و تحصلنا على الجدول الآتي :

تذبذب العينات :

عندما ننجز تجربة   مرة ، نتحصل على عينة مقاسها  ، و عندما نعيد نفس التجربة  مرة في نفس الظروف نجد عينة أخرى مقاسها  ليست بالضرورة مطابقة للأولى .

تسمى هذه الظاهرة تذبذب  العينات .

تجربة عشوائية :

عندما نرمي زهر نرد غير مزيف ، و نهتم بالرقم الظاهر على وحهه العلوي ، من المؤكد أننا لا نستطيع توقع هذه النتيجة مسبقا ، إن هذه التجربة تسمى تجربة عشوائية .

المحاكاة : 

محاكاة تجربة عشوائية يعني اختيار نموذج لهذه التجربة .

أ.المجتمع 

تعريف المجتمع هو مجموعه الأفراد التي تقام عليها دراسه إحصائيه 

عدد أفراد المجتمع هو التكرار الكلي لهذا المجتمع . كل جزء من المجتمع يسمى عينه 

أمثله 

مجموعه تلاميذ ثانويه , مجموعه سيارات حظيره

ملاحظه 

عندما نتحدث عن مجتمع لا نعني بالضروره الاشخاص 

ب. الميزه 

تعريف 

نسمي ميزه إحصائيه  كل خاصيه مدروسه  على أفراد المجتمع 

تكون الميزه الإحصائيه نوعيه عندما لا تأخذ قيما عدديه 

تكون الميزه الإحصائيه كميه عندما تأخذ قيمه عاديه 

عندما تأخذ الميزه  الكميه قيما معزوله , نقول إنها متقطعه 

عندما تأخذ الميزه مالانهايه من القيم , نقول أنها مستمره 

ملاحظه 

عندما تكون الميزه كميه تسمى أيضا "متغيرا إحصائيا "

أمثله

- اللون , الشهاده ,وسيله نقل هي ميزات نوعيه

- العمر , القامه , علامه فرض , المده الزمنيه , المسافه هي ميزات كميه

- العمر , علامات الفرض , سنه الإزدياد هي ميزات كميه متقطعه

- القامه , الوزن , المسافه هي ميزه كميه مستمره