ملخص الدرس / الثالثة ثانوي/رياضيات/الدوال العددية/الدالة الأسية تغيرات و النهايات
دراسة الأسية
اتجاه تغير الدالة الأسية :
من أجل كل عدد حقيقي :
الدالة الأسية متزايدة تماما على
النهايات :
|
|
|
| |
|
|
|
|
جدول التغيرات :
|
|
|
|
|
|
|
|
|
المشتقة :
إذا كانت قابلة للاشتقاق على المجال
فإن
قابلة للاشتقاق على المجال و لدينا من أجل كل
من
:
التمثيل البياني :
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
الفيديو الثاني :
اتجاه تغير الدالة الأسية
خاصية 1:
من أجل كل عدد حقيقي
البرهان :
من أجل كل من
,
و بما أن
فإن من أجل كل
من
خاصية 2 :
الدالة الأسية متزايدة تماما على .
البرهان :
من أجل كل من
,
و منه من أجل كل
من
نتائج :
من أجل كل عددين حقيقيين و
لدينا :
يعني
و
يعني
.
من أجل كل عدد حقيقي لدينا
يعني
و
يعني
النهايات
خواص :
البرهان :
- نعتبر الدالة المعرفة على
بـ
, من أجل كل
من
,
و بما أن من أجل كل من
فإن
و منه
متزايدة تماما على
,
إذن من أجل كل من
أي
لدينا
و منه
- من أجل كل عدد حقيقي و بما أن
فإن
وفيما يلي تفاصيل اكثر في هذه الفيديوهات:
الفيديو الاول:
الفيديو الثاني:
الفيديو الثالث:
الفيديو الرابع:
الفيديو الخامس:
لدراسة نهاية الدالة نستعمل المبرهنة الخاصة بنهاية دالة مركبة .
مثال :
نعتبر الدالة المعرفة على بــ
لدينا و بما أن
فإن
أي
لدينا و بما أن
فإن
أي
وفيما يلي تفاصيل اكثر في هذا الفيديو:
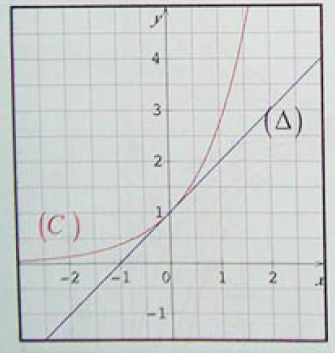
جدول تغيرات - التمثيل البياني
| |
|
| |
|
| |
|
- المنحنى الممثل للدالة الأسية يقبل محور الفواصل كمستقيم مقارب لما يؤول
الى
- لدينا و
إذن يقبل المنحني
عند النقطة ذات الفاصلة
مماسا
- من تعريف العدد المشتق لدينا : إذن
نتيجة :
الدالة هي أحسن تقريب تآلفي للدالة
بجوار
أي من أجل قريب من
لدينا
وفيما يلي تفاصيل اكثر غفي هذه الفيديوهات:
الفيديو الاول:
الفيديو الثاني:
الفيديو الثالث:
الفيديو الرابع:
اتجاه التغير ات
خاصية :
إذا كانت دالة معرفة على مجال
فإن للدالتين
و
نفس اتجاه التغيرات على المجال
.
البرهان :
نعلم أن الدالة متزايدة تماما على
. إذن حسب المبرهنة الخاصة باتجاه تغير دالة مركبة يكون للدالتين
و
نفس اتجته التغيرات على المجال
مثال :
نعتبر الدالة المعرفة على
بـ
نلاحظ أن حيث
هي الدالة المعرفة على
بـ
بما أن الدالة متناقصة تماما على المجال
فإن الدالة
متناقصة تماما على المجال
و بما أن الدالة متزايدة تماما على المجال فإن الدالة
فإن الدالة
متزايدة تماما على المجال
المشتقة
خاصية :
إذا كانت دالة قابلة للاشتقاق على المجال
فإن الدالة
قابلة للاشتقاق على
و لدينا من أجل كل
من
البرهان :
إذا كانت الدالة قابلة للاشتقاق على
و غلما أن الدالة
قابلة للاشتقاق على
فإن الدالة المركبة
قابلة للاشتقاق على
و بتطبيق قاعدة حساب مشتقة دالة مركبة يكون لدينا :
من أجل كل من
أي من أجل كل من
مثال :
- مشتقة الدالة المعرفة على
بـ
هي
- مشتقة الدالة المعرفة على
بـ
هي
الطرق المتبعة للاجابة على اسئلة الدوالك
فيما يلي دليل مختصر لالطرق المتبعة للاجابة على اسئلة الدوال في هذا الفيديو:
تطبيقات
للمزيد من التفاصيل اليك تمارين شاملة في القيديوهات التالية :
الفيديو الأول :
الفيديو الثاني :
الفيديو الثالث :
الفيديو الرابع :
الفيديو الخامس:
الفيديو السادس: