ملخص الدرس / الثالثة ثانوي/رياضيات/ المتتاليات/المتتاليات الحسابية و المتتاليات الهندسية
المتتالية الحسابية
تعريف :
عدد حقيقي نسمي متتالية حسابية ذات الأساس
كل متتالية
تحقق من أجل كل عدد طبيعي
:
مثال :
هي حدود متتالية حسابية حدها الأول
و أساسها
هو
.
تغيرات المتتالية الحسابية :
متتالية حسابية معرفة على
, حدها الأول
و أساسها
.
لدينا من أجل كل عدد طبيعي :
- إذا كان فإن المتتالية متناقصة .
- إذا كان فإن المتتالية متزايدة .
- إذا كان فإن المتتالية ثابتة .
خاصية ثلاث حدود متتابعة :
تكون الاعداد بهذا الترتيب حدود متتابعة من متتالية حسابية إذا وفقط إذا :
و
بجمع العلاقة و
نجد :
العدد يسمى الوسط الحسابي للعددين
و
حساب الحد العام لمتتالية حسابية :
إذا كان الحد الأول و أساسها
:
إذا كان الحد الأول و أساسها
:
إذا كان الحد الأول و أساسها
:
مجموع حدود متتالية حسابية :
المجموع = (عدد الحدود)*((الحد الأول +الحد الأخير)/2)
ملاحظة :
عدد الحدود (رتبة الحد الأخير -رتبة الحد الأول +1)
كيف نثبت ان المتتالية حسابية؟؟:
لاثبات ان المتتالية حسابية، نبين ان
حيث
عدد حقيقي ثابت يسمى اساس هذه المتتالية.
عبارة الحد العام:
اذا كانت معرفة على
، نحصل على
اذا كانت معرفة على
، نحصل على
العلاقة بين حدين كيفيين:
حيث
و
عددان طبيعيان من
حساب الاساس بمعرفة حدين كيفيين:
حيث
و
عددان طبيعيان متمايزان من
قانون الوسط الحسابي:
اذا كانت ،
،
حدودا متعاقبة من متتالية حسابية، فان:
اتجاه تغير متتالية حسابية:
اتجاه تغير متتالية حسابية يتبع اشارة اساسها :
1)- اذا كان ،نستنتج ان
متزايدة.
2)- اذا كان ،نستنتج ان
متناقصة.
3)- اذا كان ،نستنتج ان
ثابتة.
حساب مجموع حدود متعاقبة من متتالية حسابية:
(الحد الاخير+الحد الاول). (2/عدد الحدود)
المتتاليات الهندسية
تعريف :
عدد حقيقي , نسمي متتالية هندسية ذات الأساس
كل متتالية
تحقق من أجل كل عدد طبيعي
:
مثال :
هي حدود متتالية هندسية حدها الأول
و أساسها
هو
تغيرات متتالية هندسية :
و
فإن المتتالية
متناقصة .
و
فإن المتتالية
متزايدة.
و
فإن المتتالية
متزايدة .
و
فإن المتتالية
متناقصة .
فإن المتتالية
ثابتة .
خاصية ثلاث حدود متتابعة :
تكون الأعداد غير المعدومة بهدا الترتيب حدود متتابعة من متتالية هندسية إذا و فقط إذا :
و
بضرب العلاقة و
نجد :
حساب الحد العام لمتتالية هندسية :
إذا كان الحد الأول و أساسها
:
إذا كان الحد الأول و أساسها
:
إذا كان الحد الأول و أساسها
:
مجموع حدود متتالية هندسية :
المجموع = (الحد الأول)*(( الأساس أسعدد الحدود -1)/(الأساس -1))
ملاحظة :
عدد الحدود (رتبة الحد الأخير -رتبة الحد الأول +1)
نهاية متتالية هندسية :
و
فإن :
و
فإن :
فإن :
فإن المتتالية
متباعدة (لاتقبل تهاية)
كيف نثبت ان المتتالية هندسية؟:
لاثبات ان المتتالية هندسية، نبين ان
حيث
عدد حقيقي ثابت يسمى اساس هذه المتتالية.
عبارة الحد العام:
اذا كانت معرفة على
، نحصل على
.
اذا كانت معرفة على
، نحصل على
العلاقة بين حدين كيفيين:
حيث
و
عددان طبيعيان من
و
قانون الوسط الهندسي:
اذا كانت ،
،
حدودا متعاقبة من متتالية هندسية، فان:
اتجاه تغير متتالية هندسية:
نلخص اتجاه تغير متتالية هندسية اساسها
فيما يلي:
1)- اذا كان حدها الاول معدوما، نستنتج ان ثابتة.
2)- اذا حدها الاول غير معدوم، نميز ثلاث حالات:
- اذا كان
، نستنتج ان
مستقرة.
- اذا كان
، نستنتج ان
غير رتيبة.
- اذا كان
، فاتجاه تغير
يتبع اشارة المقدار:
.الحد الاول ، بحيث:
*اذا كان .الحد الاول، نستنتج ان
متزايدة.
* اذا كان .الحد الاول، نستنتج ان
متناقصة.
* اذا كان . الحد الاول، نستنتج ان
ثابتة.
ملاحظة:
الحالتان 2 و 3 هما الاكثر شيوعا في تمارين المتتاليات الهندسية، فينبغي التركيز عليهما.
حساب مجموع حدود متعاقبة من متتالية هندسية:
نستعمل القانون الموالي:
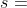 الحد الاول
الحد الاول 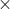 (qعدد الحدود
(qعدد الحدود 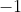 /q
/q 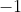 ) ;
) ; 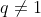
كما يمكن استخدام القانون التالي، سواء بسواء:
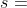 الحد الاول
الحد الاول 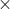 (
( 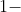 qعدد الحدود /
qعدد الحدود / 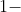 q ) ;
q ) ; 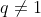
الحد الاول
ملاحظة1:
اذا اردنا الحصول على عبارة المجموع بشكل انسب فينبغي ان ننظر الى والحد الاول، فمثلا، لو كان
والحد الاول سالبا، فيفضل استخدام القانون الاول هكذا.
ملاحظة2:
في حالة متتالية هندسية ثابتة، نستخدم القانون التالي:
, الحد الاول
عدد الحدود
7. نتائج تتعلق بالمتتاليات الهندسية:
اذا كانت و
متتاليتين هندسيتين اساسهما
و
وحداهما الاولان
و
على الترتيب مع
، فان:
1)- متتالية هندسية اساسها
و حدها الاول
.
2)- متتالية هندسية اساسها
و حدها الاول
.
3)- متتالية هندسية اساسها
و حدها الاول
.
4)- متتالية هندسية اساسها
و حدها الاول
.
خلاصة
| المتتالية الهندسية | النتتالية الحسابية | المتتالية |
| المتتالية |
المتتالية |
تعريفها |
| |
|
عبارة الحد العام |
| |
|
عبارة الحد العام |
| |
|
العلاقة بين حدين مختلفين من المتتالية |
| رتبة الحد = دليل الحد + 1 |
رتبة حد إذا كان الحد الأول |
|
| رتبة الحد = دليل الحد |
رتبة حد إذا كان الححد الأول |
|
|
|
|
|
| |
|
مجموع حدود متتابعة للمتتالية |
| |
|
|
| |
|
|
|
إذا كان إذا كان إذا كان إذا كان |
إذا كان إذا كان إذا كان |
اتجاه تغير |