ملخص الدرس / الثالثة ثانوي/رياضيات/الدوال العددية/المستقيمات المقاربة الموازية لأحد محوري الاحداثيات
الملخص
من الأستاذ(ة) جبايلي محمدالمستقيم المقارب العمودي
في كل ما يلي:يرمز الى مجموعة تعريف دالة
, اما
فيرمز الى منحناها في معلم متعامد و متجانس ⟨o,i,j⟩
ملاحظة : اذا كتبنا ∞ فنقصد او
اذا كان=&space;\infty) فان تفسيرها البياني او الهندسي هو:المنحنى
فان تفسيرها البياني او الهندسي هو:المنحنى 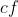 بقبل مستقيم مقاربا افقيا معادلته
بقبل مستقيم مقاربا افقيا معادلته 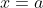 .
.
المستقيم المقارب الافقي
اذا كان فان تفسيرها البياني او الهندسي هو :
يقبل مستقيم مقاربا افقيا معادلته ,y=a و ذلك بجوار ∞.
المستقيم المقارب المائل
لاثبات ان المستقيم : (Δ) مقارب مائل ل
بجوار ∞ , يكفي ان نثبت ان :
.
اذا لم تعطي لنا معادلة المستقيم المقارب المائل ,و طلب منا تعيينه , ننظر الى عبارة ,فان كانت من الشكل التالي :
,مع
فالمستقيم ذو المعادلة مستقيم مقارب ل
عند ∞ .
اذا لم تتوفر الملاحظة السابقة , نعين المستقيم المقارب المائل باطريقة التالية :نحسب , فنجد عددا حقيقيا a غير معدوم , ثم نحسب
فنجد عددا حقيقيا b و تكون معادلة المستقيم المقارب المائل هي:
وفيما يلي تفاصيل اكثر في هذه الفيديوهات:
الفيديو الاول:
الفيديو الثاني:
الفيديو الثالث:
المنحني المقارب
اذا كان فان تفسيرها الهندسي هو:المنحنيان
و
مقاربان بجوار
نقطة النهاية
اذا كان فان تفسيرها البياني (او الهندسي ) هو: النقطة التي احداثياتها (a,b) هي نقطة نهاية للمنحنى
.
الدالة الزوجية
دالة حيث
متناظرة بالنسبة الى الصفر .لاثبات ان
زوجية , نبرهن من اجل كل
من
, ان :
ملاحظة هامة : اذا كانت زوجية , فيمكن انشاء القسم من
على الجزء الموجب ( او السالب ) من
, ثم نكمل
باتناظر بانسبة الى محور التراتيب
الدالة الفردية
دالة حيث
متناظرة بالنسبة الى الصفر . لاثبات ان
فردية,نبرهن من اجل كل
من
, ان :
او
ملاحظة هامة : اذا كانت فردية , يمكن انشاء القسم من
على الجزء الموجب (او السالب) من
,ثم نكمل
بالتناظر بالنسبة الى مبدا المعلم .
الدالة الدورية
دالة و
عدد حقيقي غير معدوم , بحيث من اجل كل
من
,
ينتميالى
. لاثبات ان
دور للدالة
نبرهن من اجل كل
من
, ان :
.
ملاحظة 1: الدور للدالة
هو اصغر عدد حقيقي موجب تماما يحقق العلاقة السابقة .
ملاحظة 2: اذا كانت دورية , فيمكن الاكتفاء بانشاء جزء من
على مجال طوله الدور
.
مركز تناظر
عدد حقيقي و
دالة , حيث
lمتناظرة بالنسبة الى
.
لاثبات ان النقطة مركز تناظر للمنحنى
, يكفي ان نثبت , من اجل كل
من
, ان :
او
.
نقطة انعطاف
بصفة عامة , اتعيين نقطة الانعطاف , نقوم بما يلي :نحسب المشتق الثاني , و ندرس اشارته , فاذا وجدنا
انعدم عنذ قيمة
من
,متغيرا اشارته ,فتكون النقطة ذات الفاصلة
نقطة انعطاف ل
حالة خاصة : في بعض الحالات , يمكن تعيين نقطة انعطاف دن اللجوء الى المشتق الثاني , و ذالك اذا انعدم المشتق الاول
عند قيمة
نقطة انعطاف ل
.
حالة اخرى : اذا كانت او
, فالتفسير الهندسي هنا هو ان النقطة ذات الفاصلة
هي نقطة انعطاف ل
.
فائدة: يكون المماس موازيا لمحور التراتيب
ملاحظة: في بعض الحالات ,يفرض علينا سياق التمرين ان نعين نقطة انعطاف بالكيفية التالية :
يطلب منا ان ندرس وضعية المنحني بانسبة الى المماس عند النقطة ذات الفاصلة
, فاذا وجدنا ان
غير وضعيته بالنسبة اى المماس ( قبل و بعد نقطة التماس ) نستنتج ان النقطة ذات الفاصلة
نقطة انعطاف ل
وفيما يلي تفاصيل اكثر في هذا الفيديو:
المماس
هناك ست صيغ -تقريبا - اطرح سؤال المماس , لكن تبقى معرفة فاصلة نقطة التماس هي المفتاح للاجابة على اى منها كما سنري .
الصيغة الاولى العادية : اكتب معادلة المماس للمنحنى عند النقطة ذات الفاصلة
.
الاجابة: نكتب الدستور :
حيث نعوض بقيمتها المعطاة .
الصيغة الثانية : اكتب معادلة المماس عند النقطة ذات الترتيب
.
الاجابة : نحل المعادلة ,وعند تعيين الحل
نكون قد عدنا الى الحالة الاولى .
الصيغة الثالثة : بين انه يوجد مماس -او اكثر - للمنحنى ميله ( او معامل التوجيه ) يساوي
.
الاجابة: نحل المعادلة , وعند تعيين الحل
( او الحلول ) نكون قد عدنا كذالك الى الحالة الاولى .
الصيغة الرابعة : بين انه يوجد مماس -او اكثر - للمنحنى , يوازى المستقيم ذا المعادلة
.
الاجابة : نحل المعادلة (عدنا الى الحالة الثالثة) .
الصيغة الخامسة : بين انه يوجد مماس - او اكثر - للمنحنى يعامد المستقيم ذا المعادلة
.
الاجابة : نحل المعادلة
الصيغة السادسة : بين انه يوجد مماس -او اكثر - للمنحنى ذات الاحداثيتين
.
الاجابة : نحل المعادلة .
عند تعيين الحل ( او الحلول ) نكون قد عدنا الى الحالة الاولى .
وفيما يلي تفاصيل اكثر في هذا الفيديو:
النقطة الزاوية
اذا كان :
و
حيث و
عدان حقيقيان (
) , فالتفسير الهندسي هو ان النقطة ذات الفاصلة
: نقطة زاوية للمنحنلى
.
ملاحظة 1 : قد نكتب النهيتان السابقتان على الشكل التالي :
و
ملاحظة 2: معادلتا نصفى المماسين عند النقطة الزاوية هما:
حيث
و مع
علما ان : و
تنبيه : تبقى النقطة الزاوية موجودة حتى لو كانت احدي النهايتين السابقتين عددا حقيقيا و الاخرى
او
استنتاج تمثيل بياني من اخر
بعد انشاء قد يطلب منا ان نستنتج منحنى اخر
-مثلا - للدالة
, ويكون الاستنتاج حسب صيغة السؤال كما سياتى :
الصيغة الاولى : استنتج حيث :
.
الاجابة :
على المجالات التى تكون فيها ( اي يكون فيها
على محور الفواصل او فوقه ).
نحصل على , و منه
نظير
على المجالات التي تكون فيها ( اي يكون فيها
تحت محور الفواصل )
نحصل على , و منه يكون
نظير
بالنسبة الى محور الفواصل .
الصيغة الثانية : استنتج منحنى
حيث :
ملاحظة : غالبا ما يطلب منا اولا ان نثبت ان زوجية .
الاجابة
اذا كان و
( الجزء الموجب من
) نحصل على
و منه
ينطبق على
.
نكمل الجزء المتبقى من بالتناظر بالنسبة الى محور التراتيب لان
زوجية.
الصيغة الثالثة : استنتج منحنى
حيث :
.
ملاحظة : غالبا ما يطلب منا اولا ان نثبت ان زوجية .
الاجابة :
اذا كان و
( الجزء السالب من
) نحصل على
; و منه
ينطبق على
.
نكمل الجزء المتبقى من بالتناظر بالنسبة الى محور التراتيب لان
زوجية .
الصيغة الرابعة :استنتج منحنى
حيث :
الاجابة :
هو نظير
بالنسبة الى محور الفواصل .
الصيغة الخامسة :استنتج منحنى الدالة
حيث :
الاجابة : هو نظير
بالنسبة الى محور التراتيب .
الصيغة السادسة : استنتج منحنى الدالة
التى تحقق
الاجابة : هو نظير
بانسبة الى مبدا المعلم .
الصيغة السابعة :استنتج منحنى الدالة
التى تحقق :
حيث
و
عددان حقيقيان
الاجابة : نستنتج ان من
بالانسحاب ذى الشعاع
الصيغة الثامنة :استنتج حيث :
الاجابة : هو نظير
بالنسبة الى المستقيم ذي المعادلة
الصيغة التاسعة : استنتج حيث:
الاجابة : هو نظير
بالنسبة الى النقطة
فيما يلي تفاصيل اكثر في هذا الفيديو:
مع حامل محور الفواصل Cf تعيين نقطة تقاطع
لتعيين احداثيات نقطة تقاطع مع حامل محور الفواصل ,نعدم
, فنحل المعادلة
, حيث
مع حامل محور التراتيب Cf تعيين نقطة تقاطع
دالة حيث
, لتعيين احداثيتي نقطة تقاطع
مع حامل محور التراتيب, نعدم
, ومن ثم نحسب
.
دراسة الوضعية النسبية لمنحنى و مستقيم
لدراسة وضعية المنحنى بالنسبة للمستقيم
ذي لبمعادلة
, نحسب العبارة
اي
و ندرس اشارتها , ونشكل جدول الوضعية
بحيث اذا كان فان
فوق
اذا كان فان
تحت
اذا كان فان
يقطع
وفيما يلي تفاصيل اكثر في هذا الفيديو:
دراسة الوضعية النسبية لمنحنيين
لدراسة وضعية المنحنى بالنسبة الى المنحنى
, نحسب العبارة
, و ندرس اشارتها ,ثم نشكل جدول الوضعية :
بحيث اذا كان فان
فوق
اذا كان فان
تحت
اذا كان فان
يقطع
نقطة التوقف
اذا كانت مستمرة عند
من اليمين فقط ,او من اليسار فقط
فالتفسير الهندسي هو: ان النقطة ذات الفاصلة , نقطة توقف ل
مثال : في الرسم المقابل النقطة نقطة توقف ل
نقطة الرجوع
دالة مجموعة تعريفها
, و
عدد حقيقي غير معزول من
و منحناها في معلم
اذا كانت :
و
او العكس بحيت تكون النهاية الاولى و الثانبة
فان
تقبل الاشتقاق عند
.
و التفسيلر الهندسي هو ان النقطة ذات الفاصلة نقطة رجوع للمنحنى
.
مثال في الرسم المقابل النقطتان A و B نقطتا رجوع ل
المناقشة البيانية
هناك ثلاثة انواع اساسية للمناقشة البيانية حسب قيم الوسيط الحقيقي m , و نذكر ها فيما يلي :
*المناقشة البيانية بمستقيم افقي :
و تكون المعادلة في هذه الحالة من الشكل :
مثل : او
او
او
او
... الى اخره
لاحظ هنا : لا يوجد للمتغير في الطرف الايمن من المعادلة
*المناقشة البيانية بميثقيم مائل :
و تكون المعادلة في هذه الحالة كالاتى :
حيث عدد حقيقي ثابت غير معدوم
مثل او
..... الى اخره
*المناقشة البيانية بمستقيم يدور حول نقطة :
و تكون المعادلة في هذه الحالة من الشكل
متل او
...الى اخره
ملاحظات :
*اقتصرنا هنا على ذكر الشكال الشهيرة
* تفاصيل كل مناقشة تعالج في التطبيقات
وفيما يلي تفاصيل اكثر في هذه الفيديوهات:
الفيديو الاول:
الفيديو الثاني:
الفيديو الثالث:
الفيديو الرابع:
الفيديو الخامس:
التنبيه في بعض الاخطاء الشائعة
اخطاء مرتكبة في مفهوم نقطة الانعطاف
يعرف البعض نقطة الانعطاف بانها النقطة التى ينعدم فيها المشتق الثانى في فاصلتها متغيرا اشارته , و هذا تعريف غير صحيح , لان انعدام المشتق الثاني مع تغير اشارته هو شرط كافى لوجود نقطة انعطاف, و ليس شرطا لازما , فقد يوجد احيانا نقطة الانعطاف, مع ان الدالة غير قابلة للاشتقاق عند فاصلة هذه النقطة ( انظر -مثلا -" حالة اخري " من الفقرة 11 في الصفحة الاولى ) اما التعريف الصحيح لنقطة الانعطاف هو: نقطة االانعطاف هى النقطة التي يخترق فيها المماس المنحنى .
اخطاء مرتكبة في مفهومي نقطتي التوقف و النهاية :
يخلط البعض بين مفهومي نقطتي التوفق و النهاية, و في الحقيقة هناك فرق شاسع بينهما , و اهم ما يميزهما عن بعضهما البعض, نقطة التوقف تنتمى الى المنحنى و يتوقف عندها ,اما نقطة النهايىة فلا تنتمي الى المنحنى بل يقترب منها .
ملاحظة: اذا اردت ان تعرف متى توجد كل نقطة منهما فانظر فقرة 5- صفحة الاولى و الفقرة 19 -الصفحة الثالثة
اخطاء مرتكبة في مفهوم القيمة الحدية :
يعرف البعض القيمة الحدية على انها صورة القيمة التى ينعدم فيها المشتق و يتغير اشارته ,و هذا تعريف غير صحيح لان انعدام المشتق مع تغيير اشارته هو شرط غير كافي لوجود قيمة حدية , و ليس شرطا لازما, بمعنى قد تقبل قيمة حدية عند
دون ان تكون
قابلة للاشتقاق عند القيمة
كحالة نقطة الرجوع - مثلا .
جدول يلخص التفسيرات الهندسية للنهايات
نهايات تتعلق بلفروع اللانهائية و نقطة النهاية :
| النهاية | التفسير الهندسي | الملاحظات |
| المستقيم ذي المعادلة |
||
| المستقيم ذو المعادلة |
|
|
| المستقيك ذو المعادلة |
|
|
|
|
المستقيم ذو المعادلة مقارب مائل |
|
| المستقيم ذو المعادلة |
|
|
| المستقيم ذو المعادلة |
|
|
| المنحنيان |
يمكن ان نقول ايضا :المنحنى |
|
| النقطة التى احداثياتها |
انتبه الى ان النقطة النهابة لا تنتمى الى المنحنى |
تابع لجدول التفسيرات الهندسية للنهايات
| الملاحظات | التفسير الهندسي | النهاية |
| النهاية تعنى ان الدالة |
المنحنى |
|
| النهاية تعنى ان الدالة |
المنحنى |
|
| النهاية تعنى ان الدالة |
المنحنى |
او |
| النهاية تعني ان الدالة |
لمنحنى |
|
| النهايتان تعنيان ان الدالة |
المنحنى |
|
|
النهايتان تعنيان ان الدالة *لاحظ هنا ان *لاحظ ايضا اننا حصلنا على نقطة زاوية حتى لو كانت احدي النهايتين عددا حقيقيا |
النقطة ذات الفاصلة |
; حيث
|
|
النهيتان تعنيان ان الدالة *لاحظ ان النقطة ذات الفاصلة * |
المنحنى |
|
|
نهايتان تعنيان ان الدالة *لاحظ هنا ان *اذا كانت النهاية الاولى |
لنقطة ذات الفاصلة |
* |
ةتطبيقات شامل
فيما يلي تطبيقات شاملة حول الدوال العددية:
تطبيق1:
الفيديو التالي يحتوي على مسألة عددية شاملة حول الدالة التناظرية:
تطبيق 2 :
تطبيق 3:
تطبيق 4:
تطبيق 5: