ملخص الدرس / الثالثة ثانوي/رياضيات/الدوال العددية/الإشتقاقية 2
تعريف
دالة عددية قابلة للإشتقاق على المجال المفتوح
و
دالتها المشتقة الأولى ، إذا كانت
قابلة للإشتقاق على المجال
فإن دالتها المشتقة تدعى الدالة المشتقة الثانية للدالة نرمز إليها بالرمز
.
مثال :
قابلة للإشتقاق على
:
و دالتها المشتقة الثانية
.
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
الفيديو الثاني :
الفيديو الثالث :
تطبيقات
للمزيد من التفاصيل اليك الفيديوهات التالية لتمارين و دروس شاملة :
الفيديو الأول :
الفيديو الثاني :
الفيديو الثالث :
الفيديو الرابع :
المشتقة و اتجاه تغير دالة
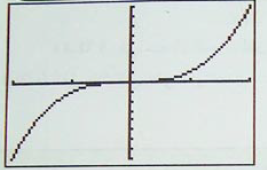
مبرهنة (دون برهان ) :
دالة قابلة للإشتقاق على المجال
من
.
- إذا كان من أجل كل من
ماعدا ممكن من أجل عدد محدود من القيم التي تنعدم االدالة
من أجلها فإن الدالة
متزايدة تماما على
,
- إذا كان من أجل كل من
ماعدا ممكن من أجل عدد محدود من االقيم التي تنعدم الدالة
من أجلها فإن الدالة متناقصة تماما على
.
-إذا كان كم أجل كل من
فإن الدالة
ثابتة على
.
ملاحظة :
لتكن الدالة المعرفة على
بــ
الدالة
قابلة للاشتقلق على
و لدينا
و منه :
من أجل كل من
و
إذن الدالة
متزايدة تماما على
.
القيم الحدية المحلية
تعاريف :
دالة معرفة على مجال
من
و
عدد حقيقي من
.
القول أن قيمة حدية محلية غظمى للدالة
يعني أنه يوجد مجال مفتوح
محتوى في
و يشمل
بحيث من أجل كل
من
.
القول أن قيم حدية محلية صغرى للدالة
يعني أنه يوجد مجال مفتوح
محتوى في
و يشمل
بحيث من أجل كل
من
القول أن قيمة حدية محلية لــــ
يعني أن
قيمة حدية محلية عظمى أو صغرى .
مثال :
لتكن الدالة المعرفة على
بـــــ
و ليكن في الشكل االمقابل تمثيلها البياني . قيمة حدية محلية عظمى للدالة
و
قيمة حدية محلية صغرى للدالة
.
مبرهنة (دون برهان ) :
دالة معرفة و قابلة لل|إشتقاق على مجال مفتوح
من
و
عدد حقيقي من
إذا انعدمت الدالة المشتقة
عند
مغيرة اشارتها فإن
قيمة حدية محلية للدالة
.
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
مشتقة الدالة u o v
مبرهنة (دون برهان )
إذا قبلت الدالة الاشتقاق على مجال
من
و قبلت الدالة
الاشتقاق على
فإن الدالة
تقبل الاشتقاق على
و لدينا من أجل كل
من
:
مثال : لتكن الدالة المعرفة على
بـــ
نلاحظ ان حيث
و
و منه
بعد الحساب نجد
مشتق الدالة :
إذا كانت الدالة قابلة للاشتقاق على مجال
من
و كانت موجبة تماما على
فإن الدالة
تقبل الاشتقاق على
و لدينا :
البرهان :
نضع و منه
حيث
الدالة تقبل الاشتقاق على
و لدينا
بما أن من أجل كل
من
,
فإن
تقبل الاشتقاق على
و لدينا
مشتقة الدالة (
عدد طبيعي يحقق
)
إذا كانت الدالة قابلة للاشتقاق على مجال
من
فإن الدالة
تقبل الاشتقاق على
و لدينا :
البرهان : نضع و منه
حيث
الدالة تقبل الاشتقاق على
و لدينا
إذن الدالة
تقبل الاشتقاق على
و لدينا :
مشتقة الدالة (
عدد طبيعي يحقق
)
إذا كانت الدالة قابلة للاشتقاق على مجال
من
و لاتنعدم على
فإن الدالة
تقبل الاشتقاق على
و لدينا
التقريب التآلفي
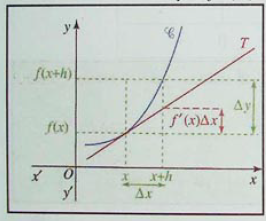
خاصية :
دالة معرفة على مجال مفتوح
.
إذا قبلت الاشتقاق عند
من
فإنه توجد دالة
بحيث من أجل كل عدد حقيقيي
حيث
ينتمي الى
لدينا مع
من أجل قريب من
نكتب عند ئذ
يسمى التقريب التآلفي لـ
من أجل
قريب من
المرفق بالدالة
.
البرهان :
ليكن من
من المعطياات لدينا
قابلة للاشتقاق عند
و منه
يكون لدينا
إذن
و منه
الكتابة التفاضلية : بوضع و
تكتب المساواة
كمايلي :
و منه التقريب عندما يكون
قريبا من
نصطلح الصياغة التفاضلية التالية : أو
يستعمل هذا الترميز في العلوم الفيزيائية و بصفة عامة نكتب : من
و
بدلا من
و هكذا بدلا من
,
طريقة أولر
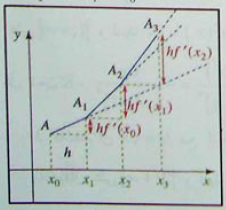
تسمح طريقة أولر بإنشاء تمثيلات بيانية تقريبية لدالة بمعرفة
و ترتكز هذه الطريقة على التقريب التآلفي للدالة
بحيث من أجل
قريب من
لدينا :
.
انطلاقا من النقطة بحيث
ننشئ النقطة
ذات الفاصلة
و التي تنتمي الى المستقيم الذي معامل توجيهه
و المار من
و بالتالي :
بما أن
من أجل
قريب من
فإن النقطة
قريبة من
منحنى
.
بنفس الطريقة يمكن إنشاء انطلاقا من النقطة
و هذا يمكن على التوالي إنشاء النقط
حيث
و
مع
بربط النقط
نحصل على تمثيل بياني تقريبي لـــ مرتبط باختيار
الذي يسمى الخطوة و نحصل على أكثر دقة كلما كان
أقرا الى
.
دراسة دالة مثلثية
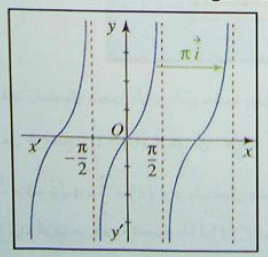
1- تذكير حول الدالتين "جيب " و "جيب تمام " :
- الدالتان و
معرفتان على
.
من أجل كل من
ينتمي الى
ينتمي
و لدينا
و
نقول أن الدالتين و
دوريتان دورهما
- من أجل كل من
;
و
2- الدالة "ظل " :
تعريف :
الدالة "ظل " و التي نرمز اليها بالرمز معرفة بــ
من أجل كل عدد حقيقي
يختلف عن
حيث
عدد صحيح
.
خواص :
*من أجل كل يختلف عن
;
إذن المنحني الممثل للدالة "ظل "دورية دورها
.
* من أجل كل يختلف عن
إذن المنحني الممثل للدالة "ظل" متناظر يالنسبة الى مبدأ المعلم
دراسة الدالة ظل :
*من الخاصيتن السابقتين يمكن اقتصار دراسة الدالة "ظل " على المجال .
* من أجل كل يختلف عن
بما أن فإن الدالة "ظل " متزايدة تماما على كل مجال معرفة فيه .
* لدينا و
و بما أن من أجل كل
من
فإن :
نستنتج أن المستقيم ذو المعادلة مستقيم مقارب للمنحنى الممثل للدالة "ظل " :
| |
|
| |
|
| |
|