ملخص الدرس / الثالثة ثانوي/رياضيات/ المتتاليات/النهايات و المتتاليات

الملخص

من الأستاذ(ة) جبايلي محمد

نهاية متتالية هندسية

قوانين النهايات المتعلقة بالمتتاليات الهندسية:

ليكن $q$ عددا حقيقيا.

*اذا كان $q\succ 1$ فان $\lim_{n \to +\infty}q^n=+\infty$

* اذا كان $-1\prec q\prec 1$ فان $\lim_{n \to +\infty}q^n=0$

* اذا كان $q\leq -1$ فان (غير موجودة) $\lim_{n \to +\infty}q^n$

ملاحظة:

تستخدم هذه القوانين لحساب النهايات في التمارين التي تتعرض للمتتاليات الهندسية، سواء تعلق الامر بالحدود العامة او المجاميع.

تقارب متتالية

*إذا كانت $\lim u_n =l$ حيث $l\in \mathbb{R}$ فإن $(u_n)$ متقاربة

*و إذا كانت $\lim u_n=+\infty$ أو $\lim u_n=-\infty$ أو $\lim u_n$ غير موجودة فإن $(u_n)$ متباعدة .

نتيجة : نظرية أخرى لمعرفة تقارب متتالية

أ- إذا كانت $(u_n)$ متزايدة و محدودة من الأعلى فإن $(u_n)$ متقاربة .

ب- إذا كانت $(u_n)$ متناقصة و محدودة من الأسفل فإن $(u_n)$ متقاربة .

حساب نهاية متتالية

هناك طريقتين :

أولا : $u_n=f(n)$ (عبارة الحد العام ) تحسب النهاية باستخدام قواعد الدوال المعروفة

ثانيا : $u_{n+1}=f(u_n)$ (علاقة تراجعية ) فإذا كانت $(u_n)$ متقاربة فإننا نحل المعادلة $f(l)=l$

ملاحظة :

في بعض التمارين المعادلة $f(l)=l$ تقبل أكثر من حل و بالتالي علينا رفض كل الحلول عدا واحد فقط و يكون سبب الرفض إما المجال الذي تنتمي اليه حدود المتتالية (المحدودية ) أو اتجاه تغيرها

تمثيل حدود متتالية على محور الفواصل

لتوضيح ذلك نأخذ تطبيق

تطبيق : $(u_n )$ متتالية عددية معرفة بحدها الأول $u_0=1$ و من أجل كل عدد طبيعي $n$ : $u_{n+1}=\sqrt{2u_n+3}$

لتكن الدالة $f$ المعرفة على المجال $\left [ -\frac {3}{2};+\infty \right [$ كمايلي $f(x)=\sqrt{2x+3}$

$(C)$ تمثيلها البياني و $(d)$ المستقيم ذو المعادلة في المستوي المنسوب الى معلم متعامد و متجانس (أنظر الشكل المقابل )

المطلوب : مثل على محور الفواصل الحدود $u_2,u_1,u_1$ و $u_3$ (دون حسابها موضحا الخطوط)

تقارب وتباعد متتاليه

تقارب وتباعد متتاليه

إذا كانت $u_{n}=l$ حيث $l\epsilon R$ فإن $(u_{n})$ متقاربه

إذا كانت $lim u_{n}=+\infty$ أو $lim u_{n}=-\infty$ أو $lim u_{n}$ غير موجوده فإن $(u_{n})$ متباعده

نتيجه

نظريه أخرى لمعرفه تقارب متتاليه

إذا كانت $(u_{n})$ متزايده ومحدوده من الأعلى فإن $(u_{n})$ متقاربه

إذا كانت $(u_{n})$ متناقصه ومحدوده من الأسفل فإن $(u_{n})$ متباعده

حساب نهايه متتاليه

هناك طريقتين

أولا $u_{n}=f(u_{n})$ (عباره الحد العام) تحسب النهايه باستخدام قواعد الدوال المعروفه

ثانيا $u_{n+1}=f(u_{n})$ (علاقه تراجعيه) فإذا كانت $(u_{n})$ متقاربه فإننا نحل المعادله $f(l)=l$

ملاحظه

في بعض التمارين المعادله $f(l)=l$ تقبل أكثر من حل وبالتالي علينا رفض كل الحلول عدا واحد فقط ويكون سبب الرفض إما المجال الذي تنتمي إليه حدود المتتاليه (المحدوديه) أو اتجاه تغيرها

المتتاليتان المتجاورتان

نقول عن المتتاليتان $u_{n}$ و $v_{n}$ إذا كانت إحداهما متزايده والأخرى متناقصه و $\lim_{n\rightarrow +\infty }(u_{n}-v_{n})=0$

ملحوظه

المتتاليتان المتجاورتان متقاربتان و $\lim_{n\rightarrow +\infty }u_{n}=\lim_{n\rightarrow +\infty }v_{n}$

تمثيل حدود متتاليه على محور الفواصل

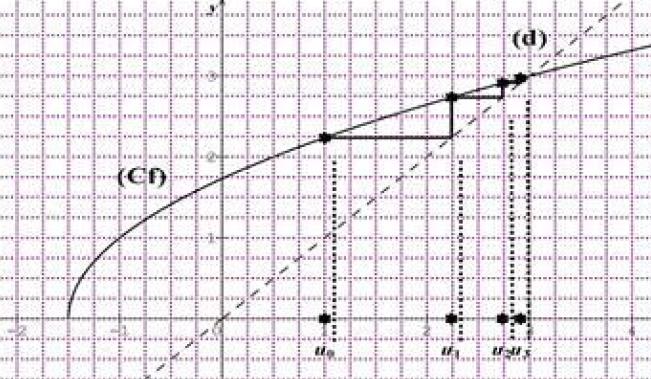
لتوضيح ذلك نأخذ تطبيق

تطبيق $u_{n}$ متتاليه عدديه معرفه بحدها الأول $u_{0}=1$ , ومن أجل كل عدد طبيعي $n$ : $u_{n+1}=\sqrt{2u_{n}+3}$

لتكن $f$ الداله المعرفه على المجال $[-\frac{3}{2};+\infty ]$ كما يلي $f(x)=\sqrt{2x+3}$ $(C)$ تمثيلها البياني و $(d)$ المستقيم ذو المعادله $y=x$ في المستوي المنسوب إلى المعلم المتعامد والمتجانس (أنظر الشكل المقابل)