ملخص الدرس / الثالثة ثانوي/رياضيات/الدوال العددية/الدالة الأسية نظريات و تعاريف
تعريف
توجد دالة وحیدة قابلة للاشتقاق على و تحقق :
و
تسمى هذه الدالة بالدالة الأسية ذات الأساس و نرمز لها بالرمز
حيث عدد حقيقي ثابت قيمته التقريبية
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
الفيديو الثاني :
الخواص الجبرية
من أجل كل عددين حقيقيين و من أجل عدد صحيح نسبي
لدينا :
العدد و الترميز
، العدد
هو صورة العدد
بالدالة الأسية أي
حيث حسابيا
إصطلاحا :
من أجل كل عدد حقيقي :
نقرأ : "أسية
"
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الاول :
الفيديو الثاني :
الفيديو الثالث :
قواعد الحساب
قواعد الحساب :
من أجل كل عددين حقيقيين و من أجل كل عدد صحيح نسبي
لدينا :
|
|
x:exp(kx)الدوال الأسية
حلول المعادلة :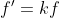
مبرهنة 1 :
ليكون عددا حقيقيا ، توجد دالة وحيدة
قابلة للاشتقاق على
بحيث :
و
هي دالة
دوال تحول المجموع إلى جداء .
مبرهنة 2 :
الدوال غير المعدومة و القابلة للاشتقاق على
بحيث : من أجل كل عددين حقيقيين
هي دوال حيث
عدد حقيقي .
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
الفيديو الثاني :
خواص و نتائج
من أجل كل عددين حقيقين و
و
عدد صحيح كيفي
* *
*
* *
*
* من أجل كل عدد حقيقي
تعميم
معناه (سالب
)
* معناه
*
معناه
*
معناه
* يكافئ
حيث
عدد حقيقي موجب تماما
النهايات الشهيرة
| الحالة العامة | الحالة الخاصة |
للمزيد من التفاصيل اليك الفيديوهات التالية :
الفيديو الأول :
قانون الإنشقاق
إذا كانت قابلة للإشتقاق على مجال
فإن
* ملاحظة : تبقى قواعد الإشتقاق المعروفة سابقا صحيحة حسب شكل الدالة المعطاة
دراسة إشارة بعض العبارات الأسية
* أولا : [ ( دالة )] هما الإشارة من إشارة الدالة
* ثانيا : في كل ممايلي , ترمز إلى أعداد حقيقية
* ثالثا : طريقة لدراسة إشارة عبارة من الشكل حيث
- إذا كان و
موجبان فإن
- إذا كان و
سالبان فإن
- إذا كان و
مختلفين في الإشارة أي
فإن للمعادلة حل يمكن إيجاد بكل بساطة ( نتمرن على ذلك التمارين ) و الإشارة بالكيفية التالية :
| |
|
* رابعا : طريقة لدراسة إشارة من الشكل حيث
لدراسة إشارة العبارة على
نقوم بمايلي :
الخطوة الأولى : نضع , فتصبح العبارة من الشكل
الخطوة الثانية : نعين قيم التي تعدمها , إن قبلت طبعا
الخطوة الثالثة : نستنتج قيم و في الأخير نشكل جدولا ندرس فيه إشارة العبارة مستخدمين الاقواعد الىمعروفة لإشارة كثيرات الحدود من الدرجة الثانية
* ملاحظة : للعبارة تحليل من الشكل
حيث
حلي المعادلة
خواص جبرية
خواص :
من أجل كل عددين حقيقين و من أجل كل عدد صحيح نسبي
لدينا :
وفيما يلي تطبيق لتفاصيل اكثر في هذه الفيديوهات:
الفيديو الاول:
الفيديو الثاني:
الفيديو الثالث:
الفيديو الرابع:
العدد e و الترميز e
* العدد هو صورة العدد
بالدالة الأسية أي
تعطينا الحاسبة
* من أجل كل عدد ىصحيح نسبي
لدينا إذن : من أجل كل عدد صحيح نسبي
اصطلاحا نرمز من أجل كل عدد حقيقي الى
بـ
من أجل كل عدد حقيقي ,
نقرأ : "
أسية
"
ملاحظة : الترميز السابق متلائم مع خواص القوى في الحالة التي يكون فيها الأس عددا صحيحا باستعمال الاصطلاح السابق تكتب خواص الدالة الأسية كمايلي :
قواعد الحساب :
من أجل كل عددين حقيقيين و من أجل كل عدد صحيح نسبي
لدينا :
حلول المعادلة f'=kf
مبرهنة :
ليكن عددا حقيقيا .
توجد دالة وحيدة قابلة للاشتقاق على
بحيث
و
هي الدالة
البرهان :
الوجود : لتكن الدالة المعرفة على
بـــ
الدالة قابلة للاشتقاق على
و لدينا من أجل كل
من
,
كما أن
و بالتالي الدالة تحقق
و
.
الوحدانية : نفرض وجود دالة ثانية قابلة للاشتقاق على
بحيث
و
نعتبر الدالة المعرفة على
بــ
الدالة قابلة للاشتقاق على
و لدينا من أجل كل
من
إذن ثابتة على
مع
و منه من أجل كل من
,
إذن من أجل كل
من
,
دوال تحول المجموع الى جداء
مبرهنة :
الدوال غير المعدومة و القابلة للاشتقاق على
بحيث :
من أجل كل عددين حقيقيين و
,
هي الدوال حيث
عدد حقيقي
البرهان :
- لتكن دالة غير معدومة و قابلة للاشتقاق على
بحيث : من أجل كل
من
,
بـأخذ و
نحصل على
أي
أي
أو
إذا كان فإن من أجل كل
من
,
مما يعني أن
معدومة و هذا مرفوض و بالتالي .
من أجل كل ثابت لدينا من أجل كل
من
,
باشتقاق الطرفين بالنسبة الى
نحصل على : من أجل كل من
من أجل
لدينا :
بوضع يكون لدينا من أجل كل
من
,
إذن
و
و منه حسب المبرهنة السابقة لدينا من أجل كل من
,
.
عكسيا :
لتكن الدالة المعرفة على
بـــ
باستعمال الخواص الجبرية للدالة الأسية نحصل على :
من أجل كل عددين حقيقيين و
,
درس شامل
فيما يلي درس شامل حول الدالة الاسية في هذا الفيديو:
تطبيقات
للمزيد من التفاصيل اليك الفيديوهات التاللية :
الفيديو الأول
مثال تطبيقي حول حل المساواة والمتراجحات لدالة اسية في هذا الفيديو: