ملخص الدرس / الثالثة ثانوي/رياضيات/الإحصاء و الإحتمالات /العد القوائم الترتيبات التبديلات
الملخص
من الأستاذ(ة) عبعوب محمدما يجب معرفته
1- العاملي :
مثال :
حساب مايلي : عاملي
لاتنسى : و
2- الترتيبة:
مثلا لحساب :
لاتنسى و
3- التوفيقة : وتحسب بالطريقة التالية :
مثلا لحساب :
دون أن تنسى : و
4- التبديلة :
قانون حسابها :
5- القائمة :
قانون حسابها :
العد (القوائم , الترتيبات , التبديلات )
1- قوائم عناصر مجموعة منتهية :
تعريف :
مجموعة منتهية ذات
عنصرا
و
عدد طبيعي
نسمي قائمة ذات عنصرا من
كل متتالية من
و عنصرا من عناصر
إذا أردنا أن تكون هذه العناصر المرتبة متمايزة مثنى مثنى عندئذ لا يمكن للقائمة أن تحتوي أكثر من عنصرا و هذا ما يقتضي أن يكون
.
* من أجل كل عدد طبيعي عدد قوائم
ذات
عنصرا يساوي
بينما يكون عدد قوائم
ذات
عنصرا المتمايزة العناصر مثنى مثنى هو
هذا الجداء يحوي
عاملا
2- التفسير :
في الحالة الأولى (عدم اشتراط تمايز العناصر ) يكون لكل عنصر من عناصر القائمة امكانية و منه فإن عدد القوائم هو (
مرة ) أي
في الحالة الثانية (قوائم عناصرها متمايزة مثنى مثنى ) يكون للعنصر الأول امكانية ثم
امكانية للعنصر الثاني و
للعنصر الثالث
و أخيرا
امكانية للعنصر الأخير الذي رتبته
باستعمال مبدأ الضرب يكون عند هذه القوائم
ملاحظة : نسمي القائمة التي عناصرها متايزة مثنى مثنى ترتيبة و يرمز لعدد الترتيبات ذات عنصرا من بين
عنصرا بالرمز
و نكتب
مثال:
1) ما عدد الأعداد ذات أرقام و التي يمكن تشكيلها من الأرقام
؟
2) ما عدد الأعداد ذات أرقام متمايزةمثنى مثنى و التي يمكن تشكيلها من الأرقام
؟
الحل :
1) كل عدد هوقائمة ذات عناصر بين الأرقام
عدد الأعداد هو
2) كل عدد هو ترتيبة ذات عناصر متمايزة من بين الأرقام
عدد الأرقام هو
3- تعريف :
ترتيبة ذات عنصرا من مجموعة ذات
عنصرا تسمى تبديلة ذات
عنصرا عدد التبديلات إذن هو
و يرمز له بالرمز
و يقرا مفكوك
أو (
عاملي )
ملاحظة :
يمكن كتابة عدد الترتيبات ذات عنصرا من مجموعة ذات
عنصرا يبالشكل
التوفيقات - دستور ثنائي الحد
1- تعريف :
مجموعة منتهية ذات
عنصرا
و
عدد طبيغي حيث
نسمي توفيقة ذات
عنصرا من عناصر
كل جزء من
ذي
عنصرا من عناصر
نرمز لعدد التوفيقات ذات عنصرا من مجموعة ذات
عنصرا بالرمز
أو الرمز
* نلاحظ أن أي أن عدد الأجزاء التي تحتوي عنصرا واحدا من مجموعة ذاات
عنصرا هو
بينما
إذ لايوجد إلا جزء واحد يحوي كل العناصر و هو المجموعة نفسها و كذلك
لأن الجزء الوحيد الذي لا يحوي أي عنصر هو الجزء الخالي
مبرهنة 2 :
من أجل كل عددين طبيعيين و
حيث
تفسير : من كل توفيقة ذات عنصرا يمكن تشكيل
ترتيبة ذات
عنصرا . لكن عدد الترتيبات ذات
عنصرا من مجموعة ذات
عنصرا هو
و بالتالي
مثال :
نريد تشكيل لجنة ذات تلاميذ من بين
تلميذا , ما عدد اللجان الممكن تشكيلها ؟
* كل لجنة هي توفيقة ذات عناصر من بين
عنصر و بالتالي فإن عدد اللجان هو
3- خواص :
1) من أجل كل عددين طبيعيين و
حيث
لدينا
2) من أجل كل عددين طبيعيين و
حيث
لدينا
تفسير :
1) عدد الأجزاء التتي تحوي عنصرا هو عدد متمماتها التي تحوي
عنصرا .
2) عدد الأجزاء ذات عنصر التي تحوي العنصر
هو
و عدد الأجزاء ذات عنصرا و التي لا تحتوي العنصر
هو
و بالتالي فعدد الأجزاء ذات
عنصر هو
و هو
.
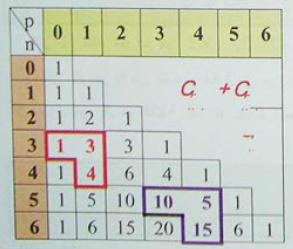
ملاحظة :
تمكننا الخاصية الثانية من حساب إذا علمنا
و
كما هو مبين من الشكل
4- دستور ثنائي الحد:
و
عددان طبيعيان
عدد طبيعي
لدينا
نمذجة تجربة عشوائية
عندما يكون عدد مخارج تجربة عشوائية منتهيا , نعرف على مجموعة المخارج قانون احتمال و ذلك باعطاء متتالية أعداد
تحقق
و
من أجل كل
مثال :
يحتوي صندوق كريات (ثلاثة منها تحمل الرقم
وكريتان تحملان الرقم
و كرية تحمل الرقم
)
الكريات لا نكيز بينها عند اللمس نسحب عشوائيا كرية واحدة
هناك عدة اختبارات ممكنة للأعداد تحقق الشروط السابقة لكن النموذج المختار لا كون مناسب إلا في حالة اقتراب التكرارات الاحصائية من الأعداد
عندما يكون عدد التجارب أكبر
إن الحدس يقودنا الى النموذج التالي :
* في حالة تساوي الأعداد نقول أن قانون الإحتمال متساوي التوزيع (أونقول تساوي الاحتمال )
أي (من أجل كل لدينا
* نذكر أن أمل قانون الاحتمال هو العدد تباينه العدد
و انحرافه المعياري هو العدد
* و نذكر أن الحادثة هي كل جزء من و أن
تدعى حدثة أولية .
الحادثة الاكيدة و
هي الحادثة المستحيلة
* احتمال حادثة هو مجموع احتمالات كل المخارج التي تنتمي الى
و في حالة تساوي احتمال يؤول حساب احتمال
أي
الى مسألة عد .
مبرهنة :
في حالة تساوي احتمال على يكون لدينا من أجل كل حادثة
عددعناصر / عدد عناصر
أخيرا نذكر ببعض الخواص :
| أجزاء |
لغة الحوادث | الخاصية |
| |
|
|
| |
الحادثتان الاكيدة و المستحيلة | |
| |
|
|
| |
|
|
| |
|
|
المتعير العشوائي , الأمل الرياضي و التباين لمتغير عشوائي
متغير عشوائي هو دالة عددية عرفة على مجموعة المخارج
و مزودة باحتمال
يأخذ القيبم
بالاحتمالات
معرف كمايلي
إرفاق القيم بالقيم
هوتعريف قانون احتمال جديد على
هذا القانون يرمز له بـ
أو
و يسمى قانون
الأمل الرياضي لمتغير عشوائي هو الأم الرياضاتي لقانون احتماله
و كذلك التباين والانحراف المعياري و نرمز لها على الترتيب بالرموز
* خواص الأمل الرياضاتي و التباين لمتغير عشوائي :
هو معدل القيم
مرفقة بالقيم
بالمقارنة مع مجال الاحصاء
هو
و في ميدان الألعاب هو الربح المتوسط الذي يأمله اللاعب بعد تكرار اللعبة مرات كثيرة , فانعدام
يدل على أن اللعبة عادلة و
يعني أن اللعية مربحة و في حالة
فهي ليست في مصلحة اللاعب كما في مجال الاحصاء فإن التباين و الانحراف المعياري مقياس تشتت .
يمكن ان نبرهن بسهولة مايلي :
مبرهنة :
و
متغيران عشوائيان معرفان على نفس الوضعية و
عدد حقيقي لدينا
و
حيث و
هما الأملان الرياضياتيان لكل من
و
ينتج من المبرهنة السابقة الخواص التالية :
متغير عشوائي و
عددان حقيقيان لدينا :
و
و
ملاحظة : برهان ما سبق ينتج مباشرة من التعريف (بحسابات بسيطة نتحقق من المتساويات في المبرهنة و الخواص )
الاحتمالات الشرطية
1- تعريف
لتكن حادثة من مجموع المخارج
حيث
. نعرف على
احتمالا جديدا يرمزله بالرمز
حيث من أجل كل حادثة
نكتب
يسمى الاحتمال الشرطي علما أن
محققة
و نقرأ " احتمال
علما أن
محققة "
مثال :
صندوق يحوي قريصات مرقمة بالأرقام
و
قريصات مرقمة بالأرقام
لا نميز بينها عند اللمس . نسحب عشوائيا على التوالي و دون ارجاع قريصتين من الصندوق .
- ما احتمال الحصول على رقمين زوجيين ؟
الحل :
نسمي الحادثة "القريصةالمسحوبة الأولى رقما زوجيا " و
الحادثة " القريصة الثانية تحمل رقما فرديا "
واضخ أن و نريد حساب
أي
لكن
هو احتمال سحب رقما زوجيا من الصندوق الذي يحوي الا اربعة أرقام زوجية من بين
ارقام أي
و بالتالي
2- دستور الاحتمالات الكلية :
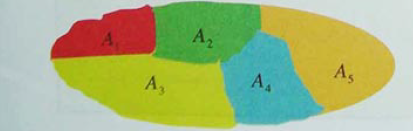
2-1 تجزئة مجموعة : نسمي تجزئة مجموعة أجزاء لهذه المجموعة كلها ليست خالية منفصلة مثنى مثنى (لا يوجد جزءان لهما عنصر مشترك ) و اتحادهما المجموعة الكلية
1)
2)
3)
2-2 لتكن حوادث احتمالاتها غير معدومة تشكل تجزئة للمجموعة الشاملة
لدينا من أجل كل حادثة
مع من أجل كل
حيث
لاحظ أن العائلة تشكل تجزئة للحادثة
.
الحوادث المستقلة و المتغيرات العشوائية المستقلة
1- تعريف :
نقول عن حادثتين و
أنهما مستقلتان إذا و فقط إذا كان
إذا كان فإن
2- تعريف :
و
متغيران عشوائيان معرفان على نفس الفضاء
لتكن قيم المتغير
و
قيم المتغير
نقول أن و
مستلان عندما تكون الحادثتان
و
مستقلتان من أجل كل
و
حيث (
و
)
* في حالة استقلال الحوادث يكون احتمال قائمة النتائج هو جداء احتمالات كل النتائج (يحصل هذا عموما في التجارب العشوائية المكررة )
* متغيران عشوائيان مرتبطان بتجربتين مختلفتين مستقلان
مثال :
نرمي مرة (
عدد طبيعي أكبر من
) حجم نرد مكعب غير مزور أوجهه مرقمة من
الى
ماهو احتمال الحادثة حيث
نحصل مر واحدة على الاقل رقم فردي
حل :
لو فكرننا في الاجابة المباشرة (الحصول على رقم فردي واحد أو رقمين فرديين فقط أو .....أو كل الأرقام فردية )
فإن الحسابسيكون طويلا ومعقدا نةعا ما , و علبيه نفضل استعمال الخاصية التي تنص على مايلي .
"مجموع احتمالي حادثتين متعاكستين يساوي "
هي الحادثة "لا نحصل على الارقام الزوجية "
و منه