ملخص الدرس / الثالثة ثانوي/هندسة ميكانيكية /الآلیات/المنطق التوفیقي

الدرس

تمهيد

*يسمح المنطق التوفيقي بتعريف حاله سير الدارات الكهربائيه , إلكترونيه وهوائيه لأنظمه آليه خلال حالات منطقيه تدعى متغيرات

*يستعمل المنطق التوفيقي متعاملات منطقيه التي تحدد العلاقه بين حالات الدخول (جزء التحكم موزعات وملتقطات ) وحالات الخروج (الجزء العملي دافعات , محركات.....) يعبر عن الحالات المنطقيه بترميز عددي ثنائي وتحدد بالجبر المنطقي المسمى بجبر "بول"

أنظمه التعداد

تسمح انظمه التعداد بكتابه عدد بصيغه قاعديه معينه , تكتب الصيغه بالعباره العامه التاليه

$A_{1}A_{2}A_{3}E'E'....A_{n}=A_{1}bn^{.}+A_{2}bn^{.}+A_{3}bn^{.}+E'E'E'.A_{n}bn-n$

$A_{1}A_{2}A_{3}E'E'A_{n}$ : عدد

$A_{1}$ : الرقم الاول من اليسار

$b$ :القاعده

$A_{n}$ : الرقم الأخير

$n$ : عدد الارقام للعدد

توجد عده أنظمه التعداد ونذكر من بينها :

- النظام العشري

النظام العشري قاعدته b=10

$b=[0.1.2.3.4.5.6.7.8.9]$

صيغه عدد في النظام العشري

مثال العدد 358

$b=10$ $n=3$

$(358)_{10}=3.10\cdot -\cdot +5.10\cdot -\cdot +8.10\cdot -\cdot$

$(358)_{10}=3.10\cdot +5.10\cdot +8.10_{\frac{1}{4}}$

- النظام الثنائي

النظام الثنائي قاعدته $b=2$ $b={1.2}$

صيغه عدد في النظام الثنائي

مثال العدد 1011 $b=2$ $n=4$

$(1011)_{2}=1.2^{4-1}+0.2^{4.2}+1.2^{4-3}+1.2^{4-4}$

$(1011)_{2}=1.2^{3}+0.2^{2}+1.2^{1}+1.2^{0}$

مرور من نظام العشري إلى النظام الثنائي

نأخذ العدد في النظام العشري ثم نجزئه بتقسيمه على عدد القاعده الثنائيه وهو العدد 2 كما يبينه المثال التالي :

لدينا عدد ثنائي $(101001)_{2}$ ونريد كتابته في النظام العشري

تجرى العمليه كالتالي

$(101001)_{2}=1.2^{6-1}+0.2^{6-2}+1.2^{6-3}+0.2^{6-4}+0.2^{6-5}+1.2^{6-6}$

$(101001)_{2}=2^{5}+0+2^{3}+0+0+1.1=32+16+1$

$(101001)_{2}=(41)_{10}$

الجبر المنطقي

الجبر المنطقي أو جبر " بول " هو المنطق المستعمل من طرف الأنظمه الآليه لتحليل وترجمه المعطيات والمعلومات والإشارات المحصل عليها

يستخدم الجبر المنطقي الاعداد في النظام الثنائي بقاعده $b={0.1}$ .تعبر القيم $0$ و $1$ عن حالتين مختلفتين

الحاله المنطقيه 1

الحاله المنطقيه 0

* صحيح

*نعم

*يعمل

*مغلق

*الكال

*مقبول

* خاطئ

* لا

* متوقف

*مفتوح

* لا شيء

* سيء

جدول الحقيقه

جدول الحقيقي هو جدول يعطي قيم متغيرات الخروج بدلاله حالات التوفيقات المناسبه لمتغيرات الدخول , عدد التوفيقات لعدد n من المتغيرات ثنائيه هو $2^{n}$ حيث

2 يمثل الحالات المنطقيه 0 و1 أما n يمثل عدد متغيرات الدخول

لمتغيره الدخول واحده نحصل على $2=2^{1}$ توفيقات وهي $0$ و $1$

لمتغيرتين نحصل على $4=2^{2}$ توفيقات وهي $01;11;10;00$

ثلاثه متغيرات نحصل على $8=2^{3}$ توفيقات وهي $000;001;010;011;100;101;110;111$

تمثيل جدول الحقيقه

متغيره واحده للدخول

S	a
	0
	1

متغيرتان للدخول

S	b	a
	0	0
	0	1
	1	0
	1	1

ثلاث متغيرات للدخول

S	c	b	a
	0	0	0
	0	0	1
	0	1	0
	0	1	1
	1	0	0
	1	0	1
	1	1	0
	1	1	1

c;b;a متغيرات الدخول

S متغيرات الخروج

ملاحظه

- في حاله أخذ القيمه 1لمتغيرات الدخول تكتب الحروف c;b;a وهكذا

- في حاله أخذ القيمه 0 لمتغيرات الدخول تكتب الحروف c;b;a وهكذا

استخراج المعادلات المنطقيه من جدول الحقيقه

نقوم بعمليه جداء متغيرات الدخول المناسبه للقيمه 1 لمتغيره الخروج ثم نجمعها للحصول على المعادله المنطقيه

المثال 1

S1	a	b
0	0	0
1	0	1
1	1	0
1	1	1

$a.\overline{b}$

$\overline{a}.b$ $S_{1}=a.\overline{b}+\overline{a}.b+ab \leftarrow$

$a.b$

المثال 2

S2	a	b	c
0	0	0	0
0	0	0	1
1	0	1	0
1	0	1	1
0	1	0	0
0	1	0	1
1	1	1	0
1	1	1	1

$\overline{a}.b.\overline{c}\leftarrow$

$a.b.\overline{c}\leftarrow$

$S2=\overline{a}.b.\overline{c}+a.b.\overline{c}+\overline{a}.b.c+a.b.c\leftarrow$

$\overline{a}.b.c\leftarrow$

$a.b.c\leftarrow$

الدوال المنطقيه الأساسيه

الدوال المنطقيه هي عباره عن معادلات جبريه منطقيه تحدد حاله متغيره الخروج ابتداءا من حاله متغيرات الدخول ولا يمكن أخذ إلا حالتين 0 و1 من بين الدوال المنطقيه الأساسيه نجد

داله (نعم) داله (لا)

داله (و) داله (أو)

جدول الحقيقة

الخلية

الدالة

s=a

S	a
0	0
1	1

(نعم) oui

يكون الخروج في الحاله 1 إذا وفقط إذا كان الدخول في الحاله 1

التركيب الهوائي

التمثيل الهوائي

جدول الحقيقه

الخليه

الداله

S=a.b

S	a
1	0
0	1

(لا) NON

يكون الخروج في الحاله 1 إذا وفقط إذا كان الدخول في الحاله 0

التركيب الهوائي

التمثيل الهوائي

جدول الحقيقه

الخليه

الداله

S=a.b

s	a	b
0	0	0
0	0	1
0	1	0
1	1	1

(و) ET

يكون الخروج في الحاله 1 إذا وفقط إذا كانت كل المتغيرات الدخول في الحاله 0

التركيب الهوائي

التمثيل الهوائي

جدول الحقيقة

الخلية

الدالة

S=a.b

s	a	b
0	0	0
1	0	1
1	1	0
1	1	1

(أو) OU

يكون الخروج في الحاله 1إذا وفقط إذا كانت إحدى أو عده متغيرات الدخول في الحاله 1

التركيب الهوائي

التمثيل الهوائي

الخلية	الدالة	الخلية	الدالة
$S=\overline{a}.\overline{b}$	(لا-أو)NOR	$S=\overline{a}+\overline{b}$	(لا-و) NAND
اللوجرام الهوائي		اللوجرام الهوائي

العلاقات الجبريه الأساسيه

النظيرة	خاصيات الجمع			خاصيات الضرب
$\overline{0}=1$ $\overline{1}=0$ إذا $a=1$ فإن $\overline{a}=0$ إذا $a=0$ فإن $\overline{a}=1$	$a+0=a$ $a+1=1$ $a+a=a$ $a+\overline{a}=1$		$0+0=0$ $0+1=1$ $1+0=1$ $1+1=1$	$a.0=0$ $a.1=a$ $a.a=a$ $a.\overline{a}=0$	$0.0=0$ $1.0=0$ $0.1=0$ $1.1=1$
الخاصية التوزيعية		الخاصية التجميعية		الخاصية التبادلية
$a.b+a.c=a(b+c)$ $(a+c)(b+c)=a.b+c$		$a(b.c)=c(a.b)$ $a+(b+c)=(a+b)+c$		$a+b=b+a$ $a.b=b.a$
نظريتا "دي مرقان " $\overline{a}+\overline{b}+\overline{c}=\overline{a.b.c}$ $\overline{a}.\overline{b}.\overline{c}=\overline{a+b+c}$
العلاقات الشهيره $a+a.b$ $a+\overline{a}.b=a+b$ $a.b+\overline{a}.c=a.b+\overline{a}.c+b.c$

1- تبسيط المعادلات بالطريقه التحليليه

يتم تبسيط المعادلات المنطقيه باستعمال العلاقات الأساسيه و العلاقات الشهيره

مثال أول تبسيط المعادله المنطقيه التاليه

$S_{1}=abc+a\overline{b}c+a\overline{b}c$

$=a\overline{b}c+a\overline{b}c=a\overline{b}c$

$S_{1}=abc+a\overline{b}c=ac(b+\overline{b})=ac.1$

$S_{1}=ac$

مثال ثاني

تبسيط المعادله المنطقيه التاليه

$S_{2}=abc+ab\overline{c}+a\overline{b}c$

$S_{2}=ab\overline{c}+abc+abc+a\overline{b}c$

$S_{2}=ab(c+\overline{c})+ac(b+\overline{b})=ab+ac$

$S_{}=a(b+c)$

2-تبسيط المعادلات بجدول "كارنو "

*تعريف جدول كارنو

جدول " كارنو" هو جدول يعطي لنا حاله متغيره الخروج بدلاله متغيرات الدخول . يحتوي الجدول على مربعات

عدد المربعات يساوي عدد التوفيقات ويساوي $2^{n}$ (يمثل $n$ عدد متغيرات الدخول) .

نعتمد في ترتيب التوفيقات على النظام الثنائي

* تمثيل جدول " كارنو "

* ملء جدول كارنو

تتم عمليه إدخال جدول " كارنو" بملء الخانات المناسبه للتوفيقات المكونه للعباره بالقيمه 1 بينما الخانات الباقيه فارغه فتملء بالقيمه 0

مثال إدخال المعادله التاليه في جدول "كارنو"

$S=\overline{a}.b+a.b$

تمثل $\overline{a}.b$ و $a.b$ القيم $1$ بالنسبه لمتغيره الخروج $S$

$:a.b=1$ تدخل القيمه $1$ في الخانه التي تستنتج من تقاطع a=1 و b=1

$:\overline{a}.b=1$ تدخل القيمه $1$ في الخانه التي تستنتج من تقاطع a=0 و b=1

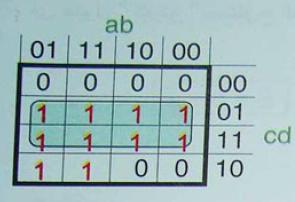
* استنتاج تبسيط المعادلات

ترتكز طريقه التبسيط بجداول "كارنو " على تجميع الخانات المتجاوره أفقيا وعموديا المملوءه بالقيمه 1 داخل مجموعات تحتوي على أكبر قوه ممكنه $2^{n}$ مع $n=1;2;3E'$

تنبيه

- تعتبر الخطوط الطرفيه المجاوره ويمكن تجميعها

- تعتبر الأعمده الطرفيه المجاوره ويمكن تجميعها

- يمكن للمجموعات أن تتقاطع أثناء عمليه التجميع

مثال

تبسيط المعادله التاليه بجدول" كارنو "

$S=\overline{a}.\overline{b}.\overline{c}+\overline{a}.\overline{b}.c +a.b.\overline{c}+a.b.c+\overline{a}.b.\overline{c}+ \overline{a}.b.c$

من جدول "كارنو" نستخرج المعادله المبسطه التاليه

$S=b+\overline{a}$

ملاحظه

تستخرج الداله المنطقيه بملء الحقيقه انطلاقا من مبدأ التشغيل جهاز آلي باحترام المراحل المختلفه ثم تبسيط هذه الداله حسابيا أو بجدول " كارنو"

مثال

حاله تشغيل جهاز آلي محدده من خلال متغيره الخروج معطاه في جدول الحقيقه الموالي

استخرج المعادله المنطقيه من جدول الحقيقه

S	d	c	b	a
0	0	0	0	0
0	0	0	0	1
0	0	0	1	0
1	0	0	1	1
0	0	1	0	0
0	0	1	0	1
0	0	1	1	0
1	0	1	1	1
1	1	0	0	0
1	1	0	0	1
1	1	0	1	0
1	1	0	1	1
1	1	1	0	0
1	1	1	0	1
1	1	1	1	0
1	1	1	1	1

$abc\leftarrow 1$

$S=a\overline{bc}\overline{d}+abc\overline{d}+\overline{a}\overline{b}\overline{c} \overline{d}+a\overline{bc}d+\overline{a}b\overline{c}d+ab\overline{c}d+\overline{a} \overline{b}cd+a\overline{b}cd+\overline{a}bcd+abcd$

$abc\leftarrow 1$

- تبسيط المعادله بجدول كارنو

"من جدول كارنو نستنتج المعادله المبسطه التاليه S=bc+d

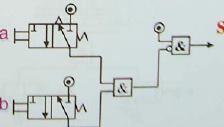
التخطيط المنطقي

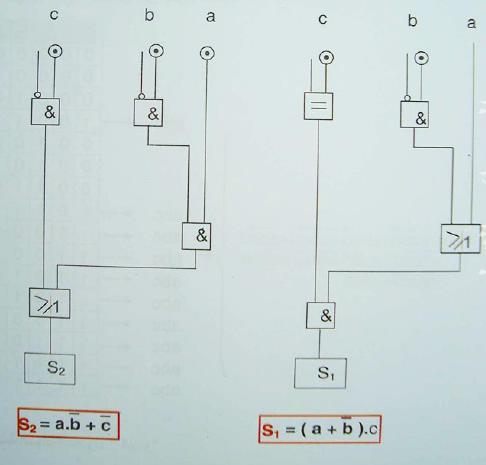
تعريف

هو تمثيل بياني مبسط لمجموعه منظمه لمتعاملات منطقيه (خلايا منطقيه) يترجم من خلاله السير المنطقي لجهاز أو نظام آلي

مثال أول مثال ثاني

المنطق التوفيقي

1- تعريف

تقام في المنطق التوفيقي دراسه المسائل المنطقيه المتعلقه بتائيه الأجهزه (الانظمه) حيث تستخرج العلاقه الموجوده بين الجزء العملي (متغيره الخروج) وجزء التحكم (متغيره الدخول)

في المنطق التوفيقي كل توفيقه لحالات متغيرات الدخول أو معلومات الدخول لا تناسب إلا لأمر واحد عند الخروج نحو الجزء العملي

يقوم نظام الآلي في المنطق التوفيقي بتفعيل المتعاملات المنطقيه الآساسيه (نعم , لا , و , أو)

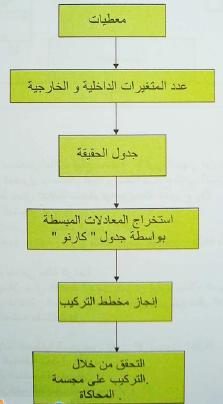
2- مراحل دراسه مسأله في المنطق التوفيقي

أستخلص

يعرف المنطق التوفيقي العلاقه المنطقيه بين متغيرات الدخول ومتغيرات الخروج.

تمثل متغيرات الدخول أنظمه التحكم (موزعات , ملتقطات)

تمثل متغيرات الخروج الأجزاء العمليه (دافعات , محركات)

تحدد المعادلات المنطقيه بالجبر المنطقي المسمى "جبر بول "

يستعمل الجبر المنطقي قاعده ثنائيه للتعداد

الدول المنطقيه الآساسيه عباره عن متعاملات منطقيه تحدد حالات الخروج ابتداءا من حالات الدخول وهي oui (نعم) . non (لا) . et (و) .ou (أو)

تحدد معادلات حالات الخروج انطلاقا من حالات الدخول بواسطه جدول الحقيقه

يكون تبسيط المعادلات المنطقيه حسابيا وبجدول "كارنو"

يوضح اللوجيغرام حاله سير جهاز آلي من خلال المتعاملات المنطقيه

تتجسد الدراسه في المنطق التوفيقي في إنشاء التركيبات (الدارات) التي تتحكم في سير الأجهزه الآليه

S	d	c	b	a
0	0	0	0	0
0	0	0	0	1
0	0	0	1	0
1	0	0	1	1
0	0	1	0	0
0	0	1	0	1
0	0	1	1	0
1	0	1	1	1
1	1	0	0	0
1	1	0	0	1
1	1	0	1	0
1	1	0	1	1
1	1	1	0	0
1	1	1	0	1
1	1	1	1	0
1	1	1	1	1

S	d	c	b	a
0	0	0	0	0
0	0	0	0	1
0	0	0	1	0
1	0	0	1	1
0	0	1	0	0
0	0	1	0	1
0	0	1	1	0
1	0	1	1	1
1	1	0	0	0
1	1	0	0	1
1	1	0	1	0
1	1	0	1	1
1	1	1	0	0
1	1	1	0	1
1	1	1	1	0
1	1	1	1	1

S	d	c	b	a
0	0	0	0	0
0	0	0	0	1
0	0	0	1	0
1	0	0	1	1
0	0	1	0	0
0	0	1	0	1
0	0	1	1	0
1	0	1	1	1
1	1	0	0	0
1	1	0	0	1
1	1	0	1	0
1	1	0	1	1
1	1	1	0	0
1	1	1	0	1
1	1	1	1	0
1	1	1	1	1