ملخص الدرس / الثالثة ثانوي/هندسة ميكانيكية /مقاومة المواد/مقاومة المواد

الدرس

تمهيد

تبين التجارب المختلفه أن المنتوجات تتحمل حمولات محدده وإذا تعدت قيم معينه , فإن هذه المنتوجات تتشوه أو تنكسر وتحدث أضرارا ولذلك تقام دراسات لتحديد هذه الحمولات حتى تضمن استعمالا مؤمنا نسمي هذه الدراسات بدراسه مقاومه المواد

التعريف

تعتبر مقاومه المواد جزء من العلوم التطبيقيه إنها تتعلق بدراسه تحليليه وتقويميه لمنتجات قصد ضمان المقاومه و الأمن

أهداف مقاومه المواد

تهدف مقاومه المواد إلى

معرفه المميزات الميكانيكيه للمواد المستعمله

دراسه مقاومه القطع الميكانيكيه

دراسه تشوه القطع الميكانيكي

المؤثرات الميكانيكيه

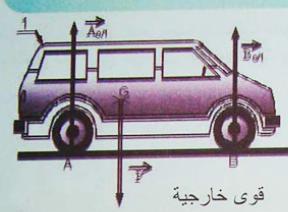
تقام دراسه مقاومه المواد انطلاقا من حمولات متمثله في مؤثرات ميكانيكيه

تعريف

نسمي مؤثره ميكانيكيه كل قوه قادره على

- تحريك جسم (أو نظام مادي)

-توقيف حركه الجسم(أو النظام المادي)

-تشويه جسم (أو نظام مادي)

1- المؤثرات الخارجيه

نسمي بالمؤثرات الخارجيه كل القوى المرثره من طرف المحيط الخارجي على النظام المادي تكون هذه المؤثرات الخارجيه

-مؤثرات عن بعد

يكون التأثير بدون تلامس الأجسام مثل الأثقال , القوى المغناطيسيه مثل $\overrightarrow{P}$

-مؤثرات التلامس

يكون التأثير في منطقه تلامس الأجسام مثل $\overrightarrow{B}_{0/1}$ و $\overrightarrow{A}_{0/1}$

2- المؤثرات الداخليه

نسمي بالمؤثرات الداخليه كل القوى المؤثره من طرف عنصر من نظام المادي على عنصر آخر من نفس النظام

تؤثر العناصر 1 و 2 و3 بعضها على بعض في نقاط التلامس A; B ;C بقوى متبادله تعدم بعضها البعض وهي

$\overrightarrow{D}_{1/3}+\overrightarrow{D}_{3/1}=\overrightarrow{O};\overrightarrow{C}_{2/3}+\overrightarrow{C}_{3/2}=\overrightarrow{O}; \overrightarrow{A}_{1/2}+\overrightarrow{A}_{2/1}=\overrightarrow{O};$

تمثل القوى العنصريه $\Delta \overrightarrow{F}_{1/2}$ و $\Delta \overrightarrow{F}_{2/1}$

قوى تماسك الجزء 1 بالجزء 2 على مستوى المقطع S

توازن جسم خاضع لمجموعه قوى مستويه

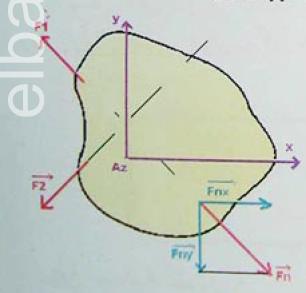
لنفترض جسم ج خاضع لمجموعه قوى خارجيه مستويه $\overrightarrow{F_{n}}....\overrightarrow{F_{2}};\overrightarrow{F_{1}}$ والنقطه $A$ من المستوي الذي تطبق فيه هذه القوى

إذا كانت محصله هذه القوى الخارجيه المطبقه على الجسم تساوي الشعاع المعدوم $\overrightarrow{F_{1}}+\overrightarrow{F_{2}}E'.\overrightarrow{F_{n}}=\overrightarrow{0}$ فإن الجسم لا ينتقل

$\overrightarrow{M_{/A\overrightarrow{F1}}}+\overrightarrow{M_{/A\overrightarrow{F2}}}.......+\overrightarrow{M_{/A\overrightarrow{Fn}}}=0$ فإن الجسم لا يدور

إذا كان الجسم ج خاضعا لمحصله معدومه للقوى الخارجيه وعزم حاصل معدوم لمجموعه عزوم هذه القوى , فإن الجسم لا يتحرك وبالتالي يكون ساكنا (أي في حاله توازن)

1- مبدأ التوازن

يكون الجسم في حاله توازن عندما يخضع ل

-محصله قوى خارجيه معدومه

-محصوله عزوم هذه القوى الخارجيه معدومه $A$

$\overrightarrow{\Sigma Fext}=\overrightarrow{0}\Rightarrow \overrightarrow{F1}+\overrightarrow{F2}........+\overrightarrow{Fn}$

$\overrightarrow{\Sigma M/A\overrightarrow{Fext}}=\overrightarrow{M/A}\overrightarrow{F1}+\overrightarrow{M/A}\overrightarrow{F2}.........+\overrightarrow{M/A}\overrightarrow{Fn}$

2-تطبيق مبدأ التوازن

-يخضع الجسم ج لنظام قوى خارجيه مستويه $\overrightarrow{Fn};.........\overrightarrow{F2};\overrightarrow{F1}$ ولتكن النقطه نقطه كيفيه من الجسم

التعبير الشعاعي

$\overrightarrow{\Sigma Fext}=\overrightarrow{0}\rightarrow \overrightarrow{F1}+\overrightarrow{F2}+......\overrightarrow{Fn}=\overrightarrow{0}$

$\overrightarrow{\Sigma M/_{A}\overline{Fext}}= \overrightarrow{M/_{A}\overrightarrow{F1}}+ \overrightarrow{M/_{A}\overrightarrow{F2}}................. +\overrightarrow{M/_{A}\overrightarrow{Fn}}=\overrightarrow{0}$

باستعمال الشعاع يتحول التعبير الهندسي إلى تعبير جبري عن طريق معادلتين تمكن من القيام بالحسابات على محور الفواصل (Ax) يكون مجموع مركبات (مساقط) القوى على (Ax) معدوما

$\overline{\Sigma Fx}=0\Rightarrow \overline{F1X}+\overline{F2X}+.......\overline{FnX}=\overrightarrow{0}$

على محور التراتيب OY, يكون مجموع المركبات (مساقط القوى) على OY معدوما

$\overline{\Sigma FY}=0\Rightarrow \overline{F1Y}+\overline{F2Y}+.......\overline{FnY}=\overrightarrow{0}$

بما أن القوى مستويه فهي تحاول تدوير الجسم على المحور Az العمودي على (Ax ;Ay)

يصبح عزم القوى ب بالنسبه للنقطه A هو نفس العزم بالنسبه للمحور (Az) وتتحول العباره الشعاعيه للعزوم إلى عباره جبريه

$\overline{\Sigma MFext/Az}=\overline{\Sigma MF/A}=0 \overline{\Sigma MF1/A}+\overline{\Sigma MF2/A}+ ..........\overline{\Sigma MFn/A}$

المد البسيط والانضغاط البسيط

تعريف

نقول على العارضه تحت تأثير قوتين منعكستين مباشره أنهاخاضعه ل

-المد البسيط عندما تؤدي هاتان القوتان إلى تمددها

- الانضغاط البسيط عندما تؤدي هاتان القوتان الى تقلصها

$\overrightarrow{M_{f}}=\overrightarrow{O} ; \overrightarrow{M_{t}}=\overrightarrow{O} ;\overrightarrow{T}=\overrightarrow{O} ;\overrightarrow{N}\neq\overrightarrow{O}$

2- إجهاد المد والإنضغاط

نفترض العارضه مقطوعه إلى جزئين 1 و 2 .نقوم بعزل الجزء 1

يكون هذا الجزء في حاله توازن تحت تأثير القوه $\overrightarrow{N}$ من جهه ومجموع قوى التماسك $\overrightarrow{\Sigma \Delta f}$ بحيث

$\overrightarrow{\Sigma \Delta f}=\overrightarrow{\Sigma \Delta f1}+\overrightarrow{\Sigma \Delta f2}..........+\overrightarrow{\Sigma \Delta fn}$

شروط التوازن

$\overrightarrow{N}=\overrightarrow{\Sigma \Delta Fn}$ $\overrightarrow{N}=-\overrightarrow{\Sigma \Delta Fn}\Leftarrow$ وبعد الإسقاط على $\overrightarrow{N}=\overrightarrow{\Sigma \Delta F}\Leftarrow O_{x}$

بما أن $S=\Delta S_{1}+\Delta S_{2}.........+\Delta S_{n}$ أي $S=\sum \Delta_{s}$ وكل $\Delta s$ يخضع لقوه $\overrightarrow{\Delta f}$

والاجهاد $\xi =N/S \Leftarrow \xi =\overrightarrow{\Sigma \Delta F}/\Delta S$ وبما أن $\overrightarrow{N}$ قوه نظاميه على المقطع القائم $(S)$ يصبح الاجهاد $\xi$ مقتصرا على الاجهاد الناظمي ونرمز له ب $\sigma$

$\sigma$ إجهاد ناظمي $(N/mm^{2})$

$N$ قوه ناظميه $(N)$

$S$ مساحه المقطع $(mm^{2})$

$\sigma =N/S$

3- التشوهات

لتكن العارضه طولها L0 وسطح مقطعها S0 تخضع هذه العارضه إلى اختبار المد الذي يبين العلاقه الموجوده القوه الناظميه $\overrightarrow{N}$ (قوه المد) واستطاله العارضه $\Delta L$

3- 1 منطقه التشوهات OA

يبين الاختيار وجود علاقه تناسب بين قوه المد واستطاله العارضه $K=F/\Delta L$ (ثابت قانون هوك) وبالتالي

$F=\Delta L/K$

في منطقه A تسمى قوه المد بقوه حد المرونه Feومنه ينتج إجهاد حد المرون $\sigma _{0}$

$\sigma _{0}=Fe/S_{0}$

وتنتج منه مقاومه حد المرونه $R_{e}$

$R_{e}=Fe/S_{0}$

المقياس الطولي للمرونه E (مقياس يونغ)

بما أن $\sigma =F/S_{0}=N/S ; F=\Delta L/K$

$\rightarrow \sigma =\Delta L/S_{0}K=L_{0}.\Delta L/L_{0}.S_{0} .K=\Delta L/L_{0}.L_{0}/S_{0}.K$

مع $\sigma =\xi .L_{0}/S_{0}.K$

( $\xi$ استطاله وحدويه)

تمثل النسبه L0/S0 ثابت خاص بالماده ويسمى E

$E=\sigma /\xi$ أو $\sigma =E.\xi$

وهو المقياس الطولي للمرونه

(مقياس يونغ)

بعض القيم ل E

الصلب $28.10^{4} N/mm^{2}\leftarrow 17.10^{4}N/mm^{2}$

الزهر $16.10^{4}N/mm^{2}\leftarrow 6.10^{4}N/mm^{2}$

النحاس $12.10^{4}N/mm^{2}\leftarrow$

الالمنيوم $7.10^{4}N/mm^{2}\leftarrow$

الخرسانه $2.10^{4}N/mm^{2}\leftarrow$

الخشب $3.10^{4}N/mm^{2}\leftarrow 4.10^{4}N/mm^{2}$

3- منطقه تشوهات BCD

ليس هناك علاقه تناسب بين قوه المد $\overrightarrow{F}$ واستطاله العارضه $\Delta L$ , العارضه لا ترجع إلى حالتها الاصليه وتبقى مشوهه وإن قوه الانكسار $\overrightarrow{Fr}$ أقل شده من القوه القصوى بسبب تقليص مساحه المقطع

4- معامل بواسون $\mu$

في مجال المرونه , توجد علاقه تناسب بين التقليص النسبي العرضي والاستطاله النسبيه الطوليه $\Delta d/d_{0}$

$\Delta d/d_{0}=\Delta L/L_{0}.\mu$

5- معامل الاستطاله %A

يعرف العامل بالعلاقه التاليه

$A=\frac{L-L_{0}}{L_{0}}\times 100$

6- معامل الانقطاع %Z

يعرف المعامل بالعلاقه التاليه

$Z=\frac{S-S_{0}}{S_{0}}$

7- شرط المقاومه

لأغراض أمنيه يبقى الاجهاد النظامي تحت قيمه محدده تسمى بالمقاومه التطبيقيه للمد أو الانضغاط $R_{p}$

$S_{max}=N/S\leq R_{p}=R_{e/s}$

مع S معامل أمن خاص بالتصميم

القص البسيط

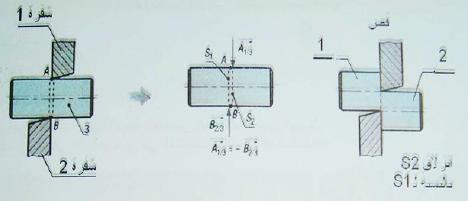
نقول على العارضه تحت تأثير قوتان متعاكستان أنها معرضه للقص البسيط عندما تؤدي هاتان القوتان إلى الانزلاق الجزء 1 على الجزء 2

$\overrightarrow{M_{F}}=\overrightarrow{O} ;\overrightarrow{M_{t}} =\overrightarrow{O}; \overrightarrow{T}\neq \overrightarrow{O} ; \overrightarrow{N}=\overrightarrow{O}$

$\zeta =\Delta f/s$

إجهاد القص

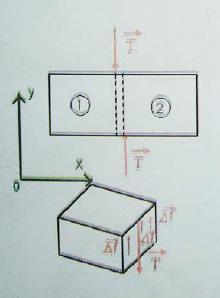
نفترض العارضه مقطوعه إلى جزئين 1 و 2 نقوم بعزل الجزء 1 . يكون هذا الجزء في حاله توازن تحت تأثير القوه $\overrightarrow{T}$ من جهه ومجموع قوى التماسك $\Sigma \overrightarrow{\Delta f}$ بحيث $\Sigma \overrightarrow{\Delta f}=\Delta f1+\Delta f2..........+\Delta fn$ شروط التوازن $T=-\Sigma \Delta f\leftarrow T+\Sigma \Delta f=0$

وبعد الاسقاط على OY نحصل على $T=\Sigma \Delta f$

بما أن $S=\Delta s1+\Delta s2.........\Delta sn$

أي $S=\Sigma \Delta s$ وكل $\Delta s$ يخضع لقوه $\overrightarrow{\Delta f}$ يصبح الاجهاد $\overrightarrow{\zeta }=\overrightarrow{T}\leftarrow \overrightarrow{\zeta }\Sigma \Delta f/\Delta s$ وبما أن $\overrightarrow{T}$ قوه مماسيه على المقطع القائم (S) يصبح الاجهاد مقتصرا على الاجهاد المماسي ونرمز ب $\tau$

$\tau =T/S$

$\tau$ إجهاد مماسي $(N/mm^{2})$

$T$ قوه مماسيه $(N)$

$S$ سطح المقطع $(mm^{2})$

التشوهات

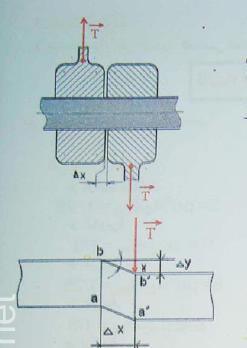
تأخذ القطعه (العارضه)بين فكين 1 , 2 الذين ينزلقان الواحد على الآخر في اختبار القص وعندما تزداد شده القوه $\overrightarrow{T}$ , يصبح المقطع ab في a'b' ويبين لنا اختبار القص العلاقه التي تربط القوه المماسيه $\overrightarrow{T}$ (قوه القص) و قيمه $\Delta x$ الانزلاق

منطقه تشوهات المرنه

يبين لنا الاختبار وجود علاقه تناسب بين قوه القص وقيمه الانزلاق $\Delta y$

$T=\Delta Y$ ثابت (قانون هول) وبالتالي

$\overrightarrow{F}=\overrightarrow{k}.\Delta Y$ في النقطه أ نسمي قوه القص بقوه حد المرونه $\overrightarrow{F_{e}}$ ومنه ينتج إجهاد حد المرونه $\overrightarrow{\zeta e}$

$\overrightarrow{\zeta }=\overrightarrow{Fe}/S_{0}$

وينتج منه مقاومه حد المرونه للانزلاق $R_{eg}$

$R_{eg}=\overrightarrow{Fe}/S_{0}$

المقياس العرضي للمرونه G (مقياس كولومب)

في منطقه المرونه تبين التجربه أن الزاويه Y صغيره جدا , إذا $Y=t_{g}Y=\Delta x/\Delta y$

$F=K/\Delta Y ;\tau =F/S=T/S\Rightarrow \tau =K\Delta Y/S=\Delta x.K\Delta Y/\Delta x.S$

$=Y.K\Delta x/S$ مع $\tau =K.\Delta x/S$ ثابت خاص بالماده ويسمى G

$\zeta =Y.G ; G=Y/\zeta$

وهو المقياس العرضي للمرونه G (مقياس كولومب)

بعض القيم ل G

-الصلب $8.10^{4}N/mm^{2}$

- الزهر $4.10^{4}N/mm^{2}$

-النحاس $4.8.10^{4}N/mm^{2}$

-الالمنيوم $3.2.10^{4}N/mm^{2}$

منطقه التشوهات اللدنه

$\zeta =F_{max}/S$

المقاومه

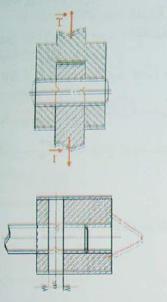
شرط المقاومه

لأسباب أمنيه , يبقى الإجهاد المماسي تحت قيمه محدده تسمى بالمقاومه التطبيقيه للإنزلاق

$\zeta maxi =T/S=R_{pg}=R_{eg}/S$

مع S معامل أمن خاص بالتصميم

4- الحالات الخاصه

تركيب بركاب

$S=pd^{2} ; R_{pg}=T/2S$

الخوبره

$S=axb ;R_{pg}=T/S$

الترزيز

$S=pd^{2} ; R_{pg}=T/2S$

اللولبه

$S=d.p.i ; R_{pg}=T/S$

برشمه

$S=pd^{2} ; R_{pg}=T/S$

علاقه بين $\zeta$ و $\sigma$

أصلاب لينه - أمزجه ألمنيوم $R_{eg}=0.5R_{e}\leftarrow$

أصناف نصف صلده $R_{eg}=0.7R_{e}$

أصلاد قاسيه أزهار $R_{eg}=0R_{e}$

الإلتواء البسيط

تعريف

نقول على عارضه تحت تأثير مزدوجتين متعاكستين أنها خاضعه للإلتواء البسيط عندما تؤدي هاتان المزدوجتان إلى التواءها

$\overrightarrow{M_{F}}=\overrightarrow{0} ;\overrightarrow{M_{t}}\neq \overrightarrow{0} ;\overrightarrow{T}=\overrightarrow{0} ;\overrightarrow{N}=\overrightarrow{0}$

1- اجهاد الالتواء

نفترض العارضه مقطوعه إلى جزئين 1 و2

نقوم بعزل الجزء 1

يكون هذا الجزء في حاله توازن تحت تأثير مزدوجه قوى من جهه ومجموع عزوم قوى التماسك من جهه أخرى

بما أن كل القوى المطبقع على العارضه مماسيه , نستلزم أن الاجهاد الناتج هو أيضا مماسي

في الالتواءالبسيط نطبق هذه العلاقه على كل سطح عنصري $\Delta s$ بحيث يطبق عليه جهد مماسي عنصري $\overrightarrow{\Delta 'F}$ إذا $\overrightarrow{Mt}+\Sigma \Phi \overrightarrow{\Delta F}=\overrightarrow{0}$ مع $\Phi$ هي المسافه بين السطح العنصري ومركز المقطع القائم

$\zeta =T/S ;Mt=\Sigma \Phi \Delta F$

التشوهات

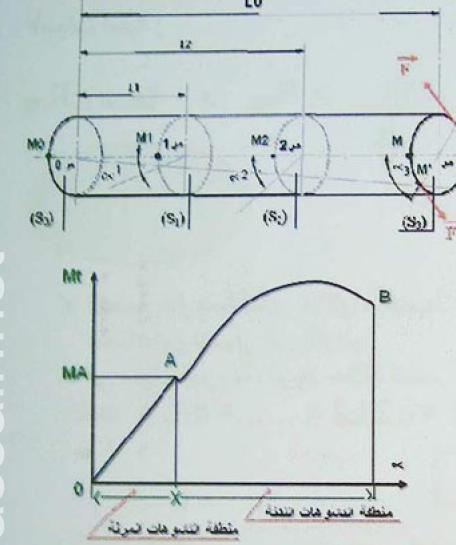
لتكن عارضه مندمجه من جهه عند تطبيق مزدوجه قوى على الطرف الثاني , تبين التجربه أن زاويه الالتواء $\alpha$ لها علاقه تناسب مع الطول $L$ في مجال المرونه

إذا تكتب العلاقه

ثابت = $\alpha _{1}/L_{1}=\alpha _{2}/L_{2}=............=\alpha /L$

ويدعى هذا الثابت بالزاويه الوحدويه للالتواء ونرمز له ب $\Theta =a/L$

في حاله توازن $\overrightarrow{Mt}+\Sigma \varphi \overrightarrow{\Delta f}=\overrightarrow{O}$ و $\zeta =\Delta f/\Delta s$ و $\zeta =G\Theta \Phi$

$\Delta f=G\Theta \Phi .\Delta s\leftarrow \Delta f=\zeta \Delta s$

إذا $Mt=\Sigma \Phi ^{2}G\Theta .\Delta s\leftarrow Mt=\Sigma \Phi G\Theta \Phi .\Delta s$

بما أن $G\Theta$ ثابت $Mt=G\Theta \Sigma \Phi ^{2}.\Delta S$ تسمى القيمه $\Sigma \Phi ^{2}.\Delta S$ بالعزم التربيعي القطبي ونرمز إليه ب $I_{0}$ إذا $Mt=G\Theta I_{0}$

$\Theta =\frac{Mt}{GI_{0}}$

بما أن $\zeta =G\theta \varphi$ و $\zeta =Mt\Phi /I_{0}\leftarrow G\Theta =Mt/I_{0}$

أو $\zeta =\frac{Mt}{\frac{I_{0}}{\Phi }}$

يصبح الإجهاد الأقصى لما يؤخذ $\Phi$ قيمه مسافه أبعد ليف بالنسبه لمحور العارضه (أي $\Phi =V$ )

$\zeta_{max} =\frac{Mt}{\frac{I_{0}}{V}}$

وتسمى النسبه $I_{0}/V$ بمقياس الإلتواء

2- شرط المقاومه

لأسباب أمنيه

$Mt/R_{pg}\leq I_{0}/V\leftarrow \frac{Mt}{\frac{I_{0}}{V }}\geq R_{pg} ;\zeta ^{max} \geq R_{PG}$

العارضه

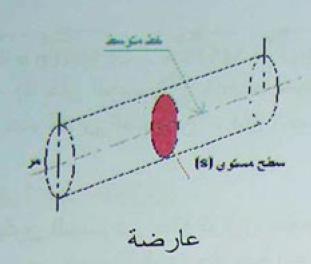
مفهوم العارضه :

نسمي عارضه في مقاومه المواد كل جسم مولد بسطح مستوي (s) حيث مركز ثقله يشكل منحنى يدعى بالخط المتوسط .

1- مميزات العارضه :

* الخط المتوسط مستقيم أو مقوس بنصف قطر كبير

* المقطع المستوي القائم ثابت أو متغير تدريجيا

* طول كبير للعارضه بالنسبه لقياساتها العرضيه

* المقطع القائم هو مقطع مستوي عمودي على الخط المتوسط للعارضه

2- فرضيات مقاومه المواد :

- تكون ماده العارضه متجانسه

- تبقى التشوهات ضعيفه مقارنه بأبعاد العارضه

- توجد القوى الخارجيه المؤثره على العارضه في مستوى تناظرها

الإجهاد

مفهوم الإجهاد

لتكن عارضه في حاله توازن تحت تأثير قوى خارجيه $\overrightarrow{F1}; \overrightarrow{F2};\overrightarrow{F3};\overrightarrow{F4}$ نقوم بقطع وهمي للعارضه إلى جزئين 1 و 2

يكون الجزء 1 في توازن تحت تأثير القوى $\overrightarrow{F1}$ و $\overrightarrow{F2}$ وقوى التماسك $\Sigma \Delta \overrightarrow{F_{1/2}}$

نسمي إجهاد Z في النقطه A لمقطع قائم (S) نهايه النسبه $\Delta \overrightarrow{F_{1/2}}/\Delta s$ عندما تؤول $(\Delta s)$ إلى الصفر

$\overrightarrow{\zeta _{A}}=Lim\frac{\overrightarrow{\Delta f_{1/2}}}{\Delta S}$

$\Delta S$ مساحه عنصريه

$\Delta f_{2/1}$ قوه تماسك عنصريه

عند اكتمال مساحه المقطع من $\Delta s$ إلى $(s)$ تجمع القوى العنصريه إلى محصله

$S=\Sigma \Delta s ; \overrightarrow{F}=\Sigma \Delta \overrightarrow{F_{2/1}}$

$\overrightarrow{F}$ بوحده نيوتن

$S$ بوحده الملمتر المربع

$\overrightarrow{\zeta}$ النيوتن على الملمتر المربع

مركبات الإجهاد

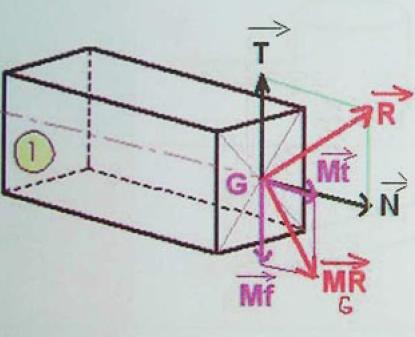
ينقسم الإجهاد $\zeta$ إلى :

* إجهاد مماسي $\tau$ منطبق على سطح المقطع القائم

* إجهاد نظامي $\overrightarrow{s}$ منطبق على سطح المقطع القائم

$\overrightarrow{\zeta }=\overrightarrow{\tau }+\overrightarrow{s}$

عناصر التبسيط على المقطع

التبسيط هو عمليه ّإختزال في مركز ثقل المقطع $G$ لمجموعه قوى خارجيه المؤثره الجزء 1 للعارضه

$\Sigma \overrightarrow{Fext}=\overrightarrow{R} \Sigma \overrightarrow{M\overrightarrow{Fext}}=\overrightarrow{M_{R}}$

تنقسم المحصله $\overrightarrow{R}$ إلى :

مركبه مماسيه للمقطع القائم وتسمى بالجهد المماسي $\overrightarrow{T}$

مركبه عموديه على المقطع القائم وتسمى بالجهد النظامي $\overrightarrow{N}$

ينقسم العزم الحاصل $\overrightarrow{M}$ إلى :

مركبه مماسيه للمقطع القائم وتسمى بالعزم الانحناء $\overrightarrow{M_{F}}$

مركبه عموديه على المقطع القائم وتسمى بعزم الالتواء $\overrightarrow{M_{t}}$

اجهادات الإنحناء البسيط

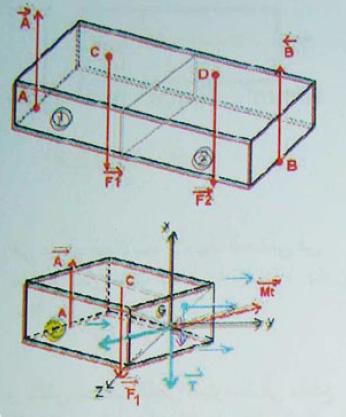
1- تعريف

نقول على عارضه تحت تأثير مجموعه قوى موجوده في مساوي تناظرها أنها خاضعه للإنحاء المستوي البسيط عندما تؤدي هذه القوى إلى انحنائها

$\overrightarrow{Mf}\neq \overrightarrow{0};\overrightarrow{Mt}=\overrightarrow{0};\overrightarrow{T}\neq \overrightarrow{0}; \overrightarrow{N}=\overrightarrow{0}$

نفترض العارضه مقطوعه إلى جزئين 1 و 2 نقوم بعزل الجزء 1 , يكون هذا الجزء في حاله توازن تحت تأثير مجموعه القوى $\overrightarrow{A}$ ; $\overrightarrow{F1}$ من جهه وقوى التماسك من جهه أخرى (محصلتها $\overrightarrow{T}$ ) في الانحناء المستوي البسيط للألياف الموجوده في المستوى الأفقي المار بمركز المقطع القائم طول ثابت (ألياف حياديه) .

الألياف الأخرى تستطيل أو تتقلص حسب وضعيتها بالنسبه للألياف الحياديه

- يتولد عن الإنحناء المستوي البسيط إجهادين

الاجهادات الناظميه $\overrightarrow{\sigma }$

الإجهادات المماسيه $\overrightarrow{\zeta }$

إجهادات ناظميه

1- التشوهات

عندما تنحني العارضه , يدور المقطع المستوي القائم بالزاويه $\varphi \Delta$ حول المحور $G_{2}Z$ , في مرحله المرونه

تبين التجربه ووجود علاقه تناسب بين $\Delta \varphi$ و $\Delta x$

$= \Delta \varphi /\Delta x$ ثابت يسمى الزاويه الوحدويه للإنحناء ونرمز لها ب $\theta$

$\theta = \Delta \varphi /\Delta x$

2- توزيع الاجهادات الناظميه على المقطع

بما أن $tg\Delta \varphi =AA'/Y$ و $tg\Delta \varphi =\Delta \varphi$

و $AA'=\Delta L$ و $\DeltaL=\varepsilon L$

إذا كان $\varepsilon =\sigma /E\leftarrow \sigma =E.\varepsilon$ و $\theta =\Delta \varphi /L$

$\sigma =Y.E.\theta \leftarrow \theta =\varepsilon /y=\sigma /yE\leftarrow$

حساب الاجهاد الناظمي الأقصى

$Mf=\Sigma \sigma \Delta s.y\leftarrow Mf=\Sigma \Delta f.Y$ ; (علاقه تناسب)

$Mf=K\Sigma Y^{2}\Delta S\leftarrow Mf=\Sigma ky.\Delta s.y$ مع $I_{GZ}=\Sigma Y^{2}\Delta s$

$\sigma =Y.Mf/I_{0}\leftarrow Mf=\sigma /Y.I_{GZ}\leftarrow$ في الحاله القصوى $y=Y$

$\sigma _{Maxi}=Mf/I_{0}/Y$ مع $I_{0}/Y$ مقياس الانحناء

2- إجهاد مماسي

في معظم الحالات , الاجهاد المماسي في مقاطع العارضات الخاضعه للإنحناء يكون ضعيفا ولا يمثل أي خطر

ونكتفي بحساب القص المتوسط في مقطع قائم , تقتصر الحسابات إلا على الجهد المماسي العرضي $\zeta m$ بينما يمثل $\zeta m$ الاجهاد المماسي الطولي الموجود على مقطع غير معني بالدراسه

إجهاد متوسط للقص $\zeta _{moy}=T/S$

الجهد القاطع

- الجهد القاطع هو الجهد المماسي المتمثل في إسقاط مجموع القوى الخارجيه على مقطع قائم

- نأخذ بعين الاعتبار إلا القوى الموجوده على يسار المقطع القائم ( $S$ ) المختار بين النقاط $C$ و $D$ على سبيل المثال $\overrightarrow{T}=\overrightarrow{A}+\overrightarrow{F1}$

عزم الإنحناء

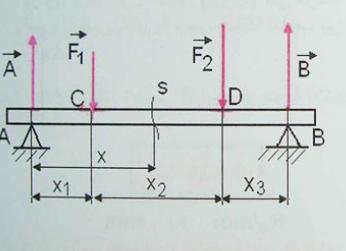
عزم الإنحناء هو إسقاط على المقطع القائم () مجموع عزوم القوى الخارجيه الموجوده على يساره

ملاحظه

الاتجاه الموجب المتفق عليه للجهود القاطعه وعزوم الانحناء يكون نحو الأسفل

مثال تطبيقي لتمثيل وحساب T وMf

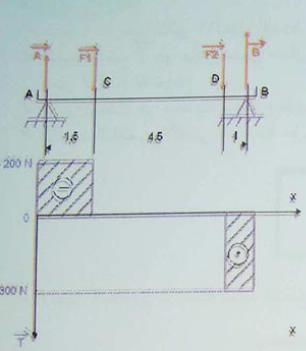
ترتكز العارضه المتمثله في الرسم المقابل على ركيزتينA وB وتتحمل مؤثرتين $\overrightarrow{F1}$ و $\overrightarrow{F2}$

نعطي $A=F1=200N ; B=F2=300N$

حساب جهود القاطعه T

منطقه $0\leq x\leq 1.5\leftarrow :AC$

$T=-A\leftarrow T=-200$

منطقه $1.5\leq x\leq 6\leftarrow :DC$

$T=-A+F\leftarrow T=0$

منطقه $6\leq x\leq 7\leftarrow :BD$

$T=-A+F1+F2\rightarrow T=+300N$

2- حساب عزوم الإنحناء

منطقه $0=x\=1.5=\leftarrow :AC$

(خط مستقيم ) $Mf=Ax$

$x=0\rightarrow Mf=0$

$x=1.5\rightarrow Mf=200.1.5=300m.N$

منطقه $1.5\leq x\leq 6\leftarrow :CD$

$MF=Ax-F1(x-1.5);X=1.5\rightarrow Mf=300m.N ;X=6\rightarrow Mf=300m.N$

منطقه $6\leq x\leq 7\leftarrow :BD$

$Mf=Ax-F1(X-1.5)-F2(x-6);X=6\rightarrow Mf=300m.N ; X=7\rightarrow Mf=0$

شرط المقاومه

لأسباب أمنيه

$R_{P}= R_{e/s}$

$\sigma_{Maxi}=\frac{Mf}{\frac{I_{0}}{Y}}\leq R_{p}$

$\zeta _{Maxi }=\frac{T_{Maxi}}{S}\leq R_{Pg}$

أستخلص

تخضع عارضه لتأثير المد البسيط عندما تكون تحت تأثير قوتين متعاكستين مباشره و أن هذه القوى تمددها

تخضععارضه لتأثير الانضغاط البسيط عندما تكون تحت تأثير قوتين متعاكستان مباشره و أن هذه القوى تقلصها

يحسب الاجهاد لناظمي بالعلاقه

يحسب شرط المقاومه بالعلاقه

$S_{max}=N/S\leq R_{p}=R_{e/s}$

يحسب معامل بواسون بالعلاقه

$\Delta d/d_{0}=\Delta L/L_{0}.\mu$

يحسب معامل الاستطاله بالعلاقه

$A=\frac{L-L_{0}}{L_{0}}\times 100$

يحسب معامل الانقطاع بالعلاقه

$Z=\frac{S-S_{0}}{S_{0}}$

في الانضغاط ولتفادي الانبعاج لا يمكن أن يتجاوز طول العارضه قياستها العرضيه بين 5 إلى 8 مرات

تخضع عارضه لتأثير القص البسيط عندما تطبق عليها قوتين متعاكستين وأن هذه القوى تحدث انزلاقا لجزء بالنسبه للجز الآخر

يحسب الإجهاد المماسي بالعلاقه

$\zeta =T/S=G.Y$

يحسب شرط المقاومه بالعلاقه

$\zeta _{max}.T/S=R_{pg}=R_{eg}/S$

العناصر المعرضه للقص المستعمله بكثره

المحاور , المرزات , البرشيم , الخوابير, الصفائح , اللولبات واللحمات

تخضع عارضه لتأثير الإلتواء البسيط عندما تطبق عليها مزدوجتي قوى متساويتين ومتعاكستين تؤديان إلى التواءها

في مجال المرونه , نوجد علاقه تناسب بين زاويه الالتواء a وطول العارضه L

ثابت $\alpha _{1}/L_{1}=\alpha _{2}/L_{2}=............=\alpha /L$ ويسمى بالتشوه الوحدوي ويرمز له ب $\Theta$

$\Theta =a/L$

الاجهاد المماسي هو جداء الزاويه الوحدويه للالتواء والمقياس G والعزم التربيعي l0

$\zeta =G\Theta L$

الزاويه الوحدويه $\Theta$ هي نسبه عزم الالتواء بجداء المقياس G مع العزم التربيعي l0

$\Theta =Mt/GI_{0}$

لحساب شرط المقاومه نستعمل العلاقه التاليه

$\zeta _{max}=\frac{Mt}{\frac{I_{0}}{V}}$

مع $I_{0}/V$ عامل الالتواء

تهدف مقاومه المواد إلى :

- معرفه المميزات الميكانيكيه

- دراسه المقاومه

- دراسه التشوه

المبدأ الأساسي للتوازن

$\Sigma \overrightarrow{Fext}=\overrightarrow{0}$

$\SigmaM \overrightarrow{Fext}=\overrightarrow{0}$

الإجهاد المماسي $\overrightarrow{\tau }$ و الإجهاد الناظمي $\overrightarrow{s}$ هما مركبات الإجتهاد $\overrightarrow{\zeta }$

عناصر التبسيط في مركز ثقل المقطع هي

- الجهد الناظمي $\overrightarrow{N}$

- الجهد المماسي $\overrightarrow{T}$

-عزم الإلتواء $\overrightarrow{Mt}$

-عزم الأنحناء $\overrightarrow{Mf}$

نقول على التأثيره أنها بسيطه إذا كان أحد عناصر التبسيط فقط غير معدوم

التأثيرات البسيطه هي

- المد البسيط $(\overrightarrow{N}\neq \overrightarrow{O})$

-الإنضغاط البسيط $(\overrightarrow{N}\neq \overrightarrow{O})$

-القص البسيط $(\overrightarrow{I}\neq \overrightarrow{O})$

-الالتواء البسيط $(\overrightarrow{Mt}\neq \overrightarrow{O})$

-الانحناء المستوي البسيط $(\overrightarrow{Mf}\neq \overrightarrow{O})$

تخضع عارضه لتأثير الإنحناء البسيط عندما تنحني تحت تأثير مجموعه قوى

الجهد القاطع هو جهد مماسي متمثل في محصله القوى الخارجيه الموجوده على يسار المقطع القائم (S)

الاجهاد الناضمي الأقصى هو نسبه عزم الانحناء على مقياس الانحناء

$\sigma_{Maxi}=\frac{Mf}{\frac{I_{0}}{Y}}$

الإجهاد المماسي هو نسبه جهد القاطع على سطح العارضه

$\zeta _{Maxi }=\frac{T_{Maxi}}{S}$

$\frac{I_{0}}{V}$ هو مقياس الانحناء

شرط المقاومه هو

$\sigma_{Maxi}=\frac{Mf}{\frac{I_{0}}{Y}}\leq R_{p}$

$\zeta _{Maxi }=\frac{T_{Maxi}}{S}\leq R_{Pg}$